题目内容
已知椭圆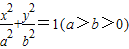
的右焦点F1，且A是椭圆上的一点，O为坐标原点，若三角形OAF1为等边三角形，则椭圆的离心率（ ）A．
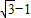
B．
C．
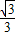
D．
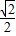
【答案】分析：利用椭圆的性质和已知即可得出△AF1F2是直角三角形，且∠AF1F2=60°.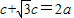
，即可得出离心率．
解答：解：设F2为椭圆的右焦点，连接AF2，由△OAF1为等边三角形，则|OA|=|OF1|=|OF2|=c，
∴△AF1F2是直角三角形，且∠AF1F2=60°．
∴
，
∴
，
∴
．
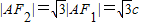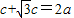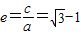故选A．
点评：熟练掌握等边三角形的性质、椭圆的标准方程及其性质是解题的关键．
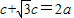，即可得出离心率．解答：解：设F2为椭圆的右焦点，连接AF2，由△OAF1为等边三角形，则|OA|=|OF1|=|OF2|=c，
∴△AF1F2是直角三角形，且∠AF1F2=60°．
∴
，∴
，∴
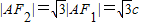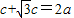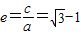．故选A．
点评：熟练掌握等边三角形的性质、椭圆的标准方程及其性质是解题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
的左焦点F1，O为坐标原点，点P在椭圆上，点Q在椭圆的右准线上，若
则椭圆的离心率为 ．
的左焦点F1，O为坐标原点，点P在椭圆上，点Q在椭圆的右准线上，若
则椭圆的离心率为 ．
的左焦点F1，O为坐标原点，点P在椭圆上，点Q在椭圆的右准线上，若
则椭圆的离心率为 ．
的左焦点F1，O为坐标原点，点P在椭圆上，点Q在椭圆的右准线上，若
则椭圆的离心率为（ ）
