Question

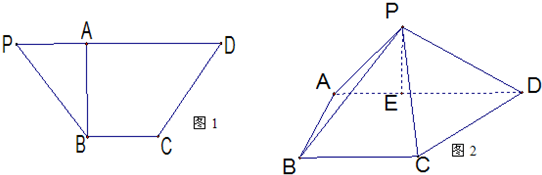
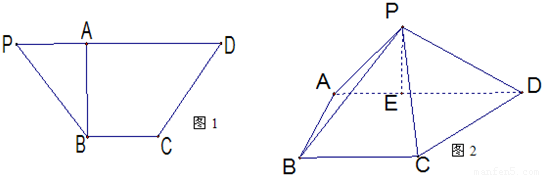
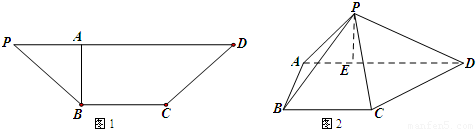
如图（图1）等腰梯形PBCD，A为PD上一点，且AB⊥PD，AB=BC，AD=2BC，沿着AB折叠使得二面角P-AB-D为60°的二面角，连接PC、PD，在AD上取一点E使得3AE=ED，连接PE得到如图（图2）的一个几何体．
（1）求证：平面PAB⊥平面PCD；
（2）求PE与平面PBC所成角的正弦值．

Answer 1

分析：（1）证明AP⊥PD，AB⊥PD，可得PD⊥平面PAB，从而可得平面PAB⊥平面PCD；
（2）连接AC，利用V_P-ABC=V_A-PBC，求出E到平面PBC的距离为h，进而利用sinθ=

h

PE

，即可求PE与平面PBC所成角的正弦值．

解答：（1）证明：∵AB⊥PA，AB⊥AD，又二面角P-AB-D为60°
∴∠PAD=60°，
又AD=2PA，∴AP⊥PD
又AB⊥平面APD，又PD?平面APD，∴AB⊥PD，
∵AP，AB?平面ABP，且AP∩AB=A
∴PD⊥平面PAB，
又PD?平面PCD，∴平面PAB⊥平面PCD---------（7分）
（2）解：设E到平面PBC的距离为h，
∵AE∥平面PBC，∴A到平面PBC的距离亦为h
连接AC，

则V_P-ABC=V_A-PBC，设PA=2
∴

1

3

×

1

2

×2×2×

3

=

1

3

×

1

2

×2×

7

×h
∴h=

2 21

7

，
 设PE与平面PBC所成角为θ，
∴sinθ=

h

PE

=

2 3 7

3

=

2 7

7

---------------（14分）

点评：本题考查面面垂直，考查线面角，解题的关键是掌握面面垂直的判定方法，利用求点面距离，求PE与平面PBC所成角．