题目内容
5.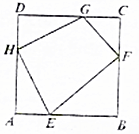 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
分析 不妨设EF=a,FG=b,GH=c,HE=d,且设DG=x,GC=1-x,CF=y,FB=1-y,BE=z,AE=1-z,AH=t,DH=1-t.由勾股定理和二次函数的最值求法:配方,即可得到最小值.
解答 解:不妨设EF=a,FG=b,GH=c,HE=d,
且设DG=x,GC=1-x,CF=y,FB=1-y,
BE=z,AE=1-z,AH=t,DH=1-t.
则2a2+b2+2c2+d2=2[z2+(1-y)2]+[y2+(1-x)2]+2[x2+(1-t)2]+[t2+(1-z)2]
=[2z2+(1-z)2]+[y2+2(1-y)2]+[2x2+(1-x)2]+[t2+2(1-t)2]
=3(z-$\frac{1}{3}$)2+$\frac{2}{3}$+3(y-$\frac{2}{3}$)2+$\frac{2}{3}$+3(x-$\frac{1}{3}$)2+$\frac{2}{3}$+3(t-$\frac{2}{3}$)2+$\frac{2}{3}$,
当x=z=$\frac{1}{3}$,y=t=$\frac{2}{3}$时,取得最小值,且为$\frac{8}{3}$.
故选D.
点评 本题考查直角三角形的勾股定理和二次函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
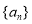 中,
中,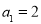 ,
,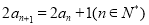 ,则
,则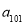 的值为( )
的值为( )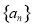 的公差为
的公差为 ,前
,前 项和为
项和为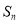 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( ) B.
B.
 D.
D.
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.