题目内容
3.抛物线y2=8x上的点(x0,y0)到抛物线焦点的距离为3,则y0=±2$\sqrt{2}$.分析 根据抛物线y2=8x可知p=4,准线方程为x=-2,进而根据抛物线的定义可知点P到其焦点的距离等于点到其准线x=-2的距离,求得点的横坐标x0,代入抛物线方程即可求得纵坐标.
解答 解:根据抛物线的方程y2=8x,可知p=4
根据抛物线的定义可知点到其焦点的距离等于点到其准线x=-2的距离,
所以得x0=1,把x0代入抛物线方程解得y0=±2$\sqrt{2}$,
故答案为:±2$\sqrt{2}$.
点评 本题考查抛物线的定义,抛物线上的点到焦点的距离,叫焦半径.到焦点的距离常转化为到准线的距离求解.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
14.圆O1:x2+y2+6x-4y+10=0与圆O2:x2+y2=4的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
11.设{an}是等差数列,{bn}是等比数列,且a1=b1,a2015=b2015,则( )
| A. | a1008>b1008 | B. | a1008≥b1008 | ||
| C. | a1008<b1008 | D. | 以上答案均有可能 |
8.对于函数y=f(x),当x∈(0,+∞)时,总有f(x)<xf′(x),若m>n>0,下列不等式中能恒成立的是( )
| A. | $\frac{f(m)}{m}<\frac{f(n)}{n}$ | B. | $\frac{f(m)}{m}>\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}>\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{n}<\frac{f(n)}{m}$ |
12.(2-x)10=a0+a1x+a2x2+…+a10x10.则a1+a2+a3+…+a10=( )
| A. | 1 | B. | -1 | C. | 1023 | D. | -1023 |
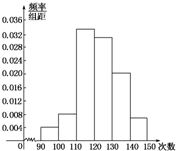 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.