题目内容
一边长为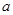 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为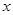 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积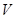 表示为
表示为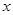 的函数;(2)
的函数;(2)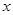 多大时,方盒的容积
多大时,方盒的容积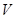 最大?
最大?
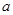 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为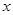 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。(1)试把方盒的容积
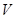 表示为
表示为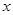 的函数;(2)
的函数;(2)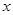 多大时,方盒的容积
多大时,方盒的容积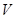 最大?
最大?(1) (2)当
(2)当 时,无盖方盒的容积
时,无盖方盒的容积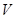 最大
最大
 (2)当
(2)当 时,无盖方盒的容积
时,无盖方盒的容积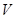 最大
最大试题分析:由于在边长为
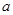 的正方形铁片的四角截去四个边长为
的正方形铁片的四角截去四个边长为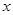 的小正方形,做成一个无盖方盒,
的小正方形,做成一个无盖方盒,所以无盖方盒的底面是正方形,且边长为
 ,高为
,高为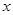 , 2分
, 2分(1)无盖方盒的容积
 5分
5分(2)因为
 ,
, .
.所以
 ,令
,令 得
得 9分
9分当
 时,
时, ;当
;当 时,
时, 11分
11分因此,
 是函数
是函数 的极大值点,也是最大值点。 12分
的极大值点,也是最大值点。 12分所以,当
 时,无盖方盒的容积
时,无盖方盒的容积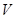 最大。 3分
最大。 3分答:当
 时,无盖方盒的容积
时,无盖方盒的容积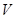 最大。 14分
最大。 14分点评:利用导数解决实际问题时,不要忘记函数本身的定义域,求最值时,要说清楚函数的单调性,步骤要完整.

练习册系列答案
相关题目
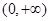 ,若对给定的正数K,定义
,若对给定的正数K,定义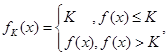 则当函数
则当函数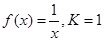 时,
时, 
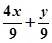
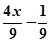
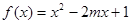 在
在 上是增函数,q:函数
上是增函数,q:函数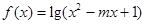 的定义域为R.
的定义域为R.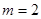 ,试判断命题p的真假;
,试判断命题p的真假;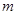 的取值范围.
的取值范围.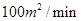 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后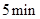 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火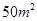 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟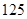 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人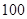 元,而每烧毁
元,而每烧毁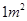 森林的损失费为
森林的损失费为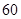 元,设消防队派了
元,设消防队派了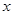 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时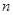
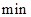 .
. 在R上可导,且满足不等式
在R上可导,且满足不等式 恒成立,且常数
恒成立,且常数 满足
满足 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )



 的定义域为R,其导函数
的定义域为R,其导函数 的图像如图所示,则对于任意
的图像如图所示,则对于任意 ,
,
 (
( ),下列结论正确的是( )
),下列结论正确的是( )
 ;③
;③ ;
; ;⑤
;⑤ 。
。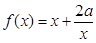
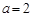 ,证明函数
,证明函数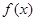 在
在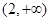 上单调递增;
上单调递增;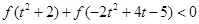 .
.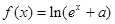 (
(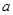 为常数,
为常数,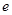 是自然对数的底数)是实数集
是自然对数的底数)是实数集 上的奇函数.
上的奇函数.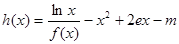 的零点的个数.
的零点的个数.