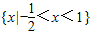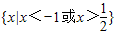题目内容

函数y=lg（2x2-x-3）的单调增区间为______．
要使函数y=lg（2x2-x-3）有意义，需满足，2x2-x-3＞0，解得，x＜-1，或x＞
3
2

∴函数的定义域为（-∞，-1）∪（
3
2
，+∞）
令t=2x2-x-3，则y=lgt，可判断当x∈（
3
2
，+∞）时，t是x的增函数，
又∵y是t的增函数，
∴复合函数y=lg（2x2-x-3）的单调增区间为（
3
2
，+∞）．
故答案为（
3
2
，+∞）．
练习册系列答案
相关题目
函数y=lg（2x2-x-1）的定义域为（　　）
函数y=lg（2x2-x-1）的定义域为
{x|x＜-
1
2
，或x＞1}．
{x|x＜-
1
2
，或x＞1}．
．
函数y=lg（2x2-x-3）的单调增区间为
(
3
2
，+∞)
(
3
2
，+∞)
．
函数y=lg（2x2-x-1）的定义域为（　　）
A．{x|-
1
2
＜x＜1}		B．{x|-
1
2
≤x≤1}
C．{x|x＜-1或x＞
1
2
}		D．{x|x＜-
1
2
或x＞1}
函数y=lg（2x2-x-1）的定义域为（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网