题目内容
已知结论“若a1,a2∈R+,且a1+a2=1,则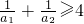 ,请猜想:若a1,a2,…an∈R+,且a1+a2+…an=1,则
,请猜想:若a1,a2,…an∈R+,且a1+a2+…an=1,则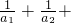 …+
…+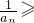 ________.
________.
n2
分析:若a1,a2∈R+,且a1+a2=1,则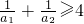 ,由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则
,由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则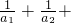
 9,从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则
9,从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则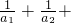 …+
…+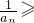 项数的平方,即可得到结论.
项数的平方,即可得到结论.
解答:若a1,a2∈R+,且a1+a2=1,则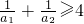 ,
,
由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则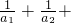
 9,
9,
从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则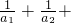 …+
…+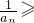 项数的平方,即可得到结论.
项数的平方,即可得到结论.
故答案为:n2.
点评:本题考查类比推理、二次函数恒成立知识,考查利用所学知识解决问题的能力.
分析:若a1,a2∈R+,且a1+a2=1,则
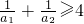 ,由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则
,由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则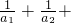
 9,从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则
9,从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则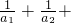 …+
…+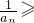 项数的平方,即可得到结论.
项数的平方,即可得到结论.解答:若a1,a2∈R+,且a1+a2=1,则
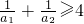 ,
,由类比推理知识得:若a1,a2,a3∈R+,且a1+a2+a3=1,则
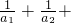
 9,
9,从而有:若a1,a2,…an∈R+,且a1+a2+…an=1,则
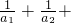 …+
…+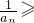 项数的平方,即可得到结论.
项数的平方,即可得到结论.故答案为:n2.
点评:本题考查类比推理、二次函数恒成立知识,考查利用所学知识解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为A1(-2,0),A2(2,0).
,且在x轴上的顶点分别为A1(-2,0),A2(2,0).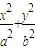 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为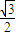 ,且在x轴上的顶点分别为A1(-2,0),A2(2,0).
,且在x轴上的顶点分别为A1(-2,0),A2(2,0). 为三个向量,则
为三个向量,则 ”
”