题目内容
(本小题12分) 已知二次函数 与
与 轴有两个交点
轴有两个交点 和
和 ,若,且
,若,且
 .
.
(Ⅰ)求此二次函数的解析式
(Ⅱ)若 在闭区间
在闭区间 的最大值为
的最大值为 ,求
,求 的解析式及其最大值
的解析式及其最大值
 与
与 轴有两个交点
轴有两个交点 和
和 ,若,且
,若,且
 .
.(Ⅰ)求此二次函数的解析式
(Ⅱ)若
 在闭区间
在闭区间 的最大值为
的最大值为 ,求
,求 的解析式及其最大值
的解析式及其最大值 (Ⅰ)
(Ⅱ) ,
,
 的最大值为4
的最大值为4

(Ⅱ)
 ,
,
 的最大值为4
的最大值为4(I)由题目条件可知 ,
,
再根据韦达定理可知 ,
, ,消去x1,x2得到关于m的不等式求出m值.
,消去x1,x2得到关于m的不等式求出m值.
(II)在(I)的基础上,此小题是属于轴定区间动的问题,然后分三种情况讨论,求出f(x)的最小值g(t),再根据求出的分段函数g(t)的解析式,分段求g(t)的最大值,最终确定g(t)的最大值.
(Ⅰ) 又
又 ,
,
由 得到
得到 ,即
,即 ,
,
 或
或 (舍去,因为
(舍去,因为 ),
),

(Ⅱ) ,
,
 的最大值为4
的最大值为4
 ,
,再根据韦达定理可知
 ,
, ,消去x1,x2得到关于m的不等式求出m值.
,消去x1,x2得到关于m的不等式求出m值.(II)在(I)的基础上,此小题是属于轴定区间动的问题,然后分三种情况讨论,求出f(x)的最小值g(t),再根据求出的分段函数g(t)的解析式,分段求g(t)的最大值,最终确定g(t)的最大值.
(Ⅰ)
 又
又 ,
,
由
 得到
得到 ,即
,即 ,
,
 或
或 (舍去,因为
(舍去,因为 ),
),

(Ⅱ)
 ,
,
 的最大值为4
的最大值为4
练习册系列答案
相关题目
 ,设函数
,设函数 ,
, ,且函数
,且函数 的值域为
的值域为 ,求
,求 在
在 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围. 的单调增区间为 ;
的单调增区间为 ;
 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;  的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数。
上是单调函数。 满足
满足 ;
; 有唯一解,求
有唯一解,求 的值;
的值; 在区间
在区间 上不是单调函数,求实数
上不是单调函数,求实数 的取值范围.
的取值范围. 在区间
在区间 上为增函数,则实数
上为增函数,则实数 的取值范围是( )
的取值范围是( )



 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.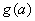 的函数表达式;
的函数表达式; 的单调增区间为_________________。
的单调增区间为_________________。