题目内容
已知数列{an}满足
，求{an}的通项公式及其前n项和Sn．
解：∵当n≥2时，an=2an-1+1，∴an+1=2（an-1+1）
=2，∴数列{an+1}为等比数列，且公比为2，
又∵a1=1，∴a1+1=2
∴an+1=2n，an=2n-1
Sn=21-1+22-1+…+2n-1=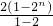
-n=2n+1-2-n
分析：根据数列的递推公式，利用构造法构造新数列满足为等比数列，求出新数列的通项公式，再求数列{an}的通项公式．
在分组求数列{an}的前n项和Sn．
点评：本题主要考查了构造法求数列的通项公式，以及分组求和．
=2，∴数列{an+1}为等比数列，且公比为2，又∵a1=1，∴a1+1=2
∴an+1=2n，an=2n-1
Sn=21-1+22-1+…+2n-1=
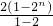-n=2n+1-2-n分析：根据数列的递推公式，利用构造法构造新数列满足为等比数列，求出新数列的通项公式，再求数列{an}的通项公式．
在分组求数列{an}的前n项和Sn．
点评：本题主要考查了构造法求数列的通项公式，以及分组求和．
练习册系列答案
相关题目