题目内容

已知函数.

(1) 判断函数f（x）在（0，上单调性；

(2) 若恒成立, 求整数的最大值；

(3) 求证：.

解：(1)

 上是减函数 4分

(2)  即h(x)的最小值大于k.

 则上单调递增,

又 存在唯一实根a, 且满足

当

∴  故正整数k的最大值是3 

(3)由(Ⅱ)知∴

令, 则  

∴ln(1＋1×2)＋ln(1＋2×3)＋…＋ln[1＋n(n＋1)]

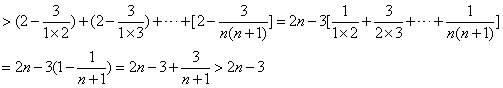
∴(1＋1×2)(1＋2×3)…[1＋n(n＋1)]＞e2n－3         

练习册系列答案
相关题目
已知函数y=
1+sinx3+cosx
，则该函数的值域是
 
．
已知函数y=
1-x
2x2-3x-2
的定义域为（　　）
已知函数(x-1)f(
x+1x-1
)+f(x)=x，其中x≠1，求函数解析式．
（2007•崇明县一模）已知函数y=-
1-x2
（-1≤x≤0）的反函数是（　　）
（2008•黄浦区一模）已知函数y=
1+bx
ax+1
(a＞0，x≠-
1
a
)的图象关于直线y=x对称．
（1）求实数b的值；
（2）设A、B是函数图象上两个不同的定点，记向量
e1
=
AB
，
e2
=(1，0)，试证明对于函数图象所在的平面里任一向量
c
，都存在唯一的实数λ1、λ2，使得
c
=λ1
e1
+λ2
e2
成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网