题目内容
已知实数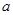 满足
满足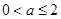 ,
,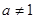 ,设函数
,设函数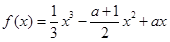
(1)当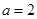 时,求
时,求 的极小值;
的极小值;
(2)若函数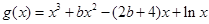 (
(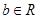 )的极小值点与
)的极小值点与 的极小值点相同,求证:
的极小值点相同,求证: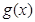 的极大值小于等于
的极大值小于等于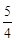
(1)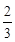 ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)把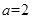 代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数
代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数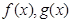 的导函数,再分
的导函数,再分 两种情况讨论,根据条件函数
两种情况讨论,根据条件函数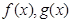 的极小值点相同分别求
的极小值点相同分别求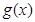 的极大值,从而进行判断得结论
的极大值,从而进行判断得结论
试题解析:(Ⅰ) 解: 当a=2时,f ′(x)=x2-3x+2=(x-1)(x-2)
列表如下:
|
x |
(- |
1 |
(1,2) |
2 |
(2,+ |
|
f ′(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以,f (x)极小值为f (2)=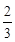 5分
5分
(Ⅱ) 解:f ′(x)=x2-(a+1)x+a=(x-1)(x-a)
g ′(x)=3x2+2bx-(2b+4)+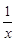 =
=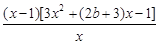
令p(x)=3x2+(2b+3)x-1,
(1)当 1<a≤2时,
f(x)的极小值点x=a,则g(x)的极小值点也为x=a,
所以pA=0,
即3a2+(2b+3)a-1=0,
即b=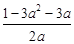 ,
,
此时g(x)极大值=g(1)=1+b-(2b+4)=-3-b
=-3+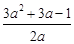 =
=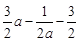
由于1<a≤2,
故 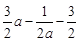 ≤
≤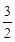
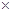 2-
2-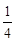 -
-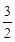 =
=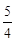 10分
10分
(2)当0<a<1时,
f(x)的极小值点x=1,则g(x)的极小值点为x=1,
由于p(x)=0有一正一负两实根,不妨设x2<0<x1,
所以0<x1<1,
即p(1)=3+2b+3-1>0,
故b>-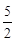
此时g(x)的极大值点x=x1,
有 g(x1)=x13+bx12-(2b+4)x1+lnx1
<1+bx12-(2b+4)x1
=(x12-2x1)b-4x1+1 (x12-2x1<0)
<-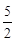 (x12-2x1)-4x1+1
(x12-2x1)-4x1+1
=-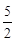 x12+x1+1
x12+x1+1
=-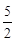 (x1-
(x1-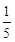 )2+1+
)2+1+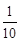 (0<x1<1)
(0<x1<1)
≤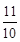 <
<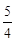
综上所述,g(x)的极大值小于等于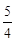 14分
14分
考点:利用导数求函数的单调性及极值

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 ,1
,1 )
) }的前n项和,记f(n)=S2n-Sn.
}的前n项和,记f(n)=S2n-Sn.