题目内容
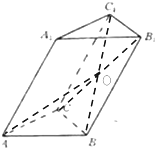 在斜三棱柱ABC-A1B1C1中,∠A1AC=∠A1AB=∠CAB=
在斜三棱柱ABC-A1B1C1中,∠A1AC=∠A1AB=∠CAB=| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:取BC的中点D,连结OD,AD,求出OD,AD,以及∠ODA,通过三角形求出AO的长度.
解答: 解:取BC的中点D,连结OD,AD,
解:取BC的中点D,连结OD,AD,
∵三棱柱ABC-A1B1C1中,∠A1AC=∠A1AB=∠CAB=
,AA1=2,AB=AC=1,
∴OD∥AA1,OD=
,AD=1,
由cos∠A1AB=cos∠A1AD•cos∠BAD,
可得cos∠A1AD=
=
=
.
在△AOD中,AO2=AD2+OD2-2AD•ODcos∠ADO
=12+(
)2-2×1×
×(-
)
=
.
∴AO=
.
故选:C.
 解:取BC的中点D,连结OD,AD,
解:取BC的中点D,连结OD,AD,∵三棱柱ABC-A1B1C1中,∠A1AC=∠A1AB=∠CAB=
| π |
| 3 |
∴OD∥AA1,OD=
| ||
| 2 |
由cos∠A1AB=cos∠A1AD•cos∠BAD,
可得cos∠A1AD=
| cos60° |
| cos30° |
| ||||
|
| ||
| 3 |
在△AOD中,AO2=AD2+OD2-2AD•ODcos∠ADO
=12+(
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
=
| 11 |
| 4 |
∴AO=
| ||
| 2 |
故选:C.
点评:本题考查空间两点距离的求法,考查空间想象能力,余弦定理的应用以及三面角公式的应用,考查计算能力.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
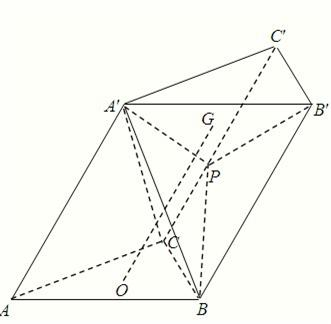 在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心.
在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC= 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 .
.