题目内容

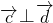已知| $数学公式$ |=1，| $数学公式$ |=2， $数学公式$ 与 $数学公式$ 的夹角为60°， $数学公式$ =2 $数学公式$ +3 $数学公式$ ， $数学公式$ =k $数学公式$ - $数学公式$ （k∈R），且 $数学公式$ ，那么k的值为

A.
-6
B.
6
C.
$数学公式$
D.
$数学公式$

D
分析：根据两个向量的垂直关系．写出两个向量的数量积等于0，根据多项式乘法法则，整理出结果，得到关于k的方程，解方程即可．
解答：∵ $\text{[math]}$ =2 $\text{[math]}$ +3 $\text{[math]}$ ， $\text{[math]}$ =k $\text{[math]}$ - $\text{[math]}$ （k∈R），且 $\text{[math]}$ ⊥ $\text{[math]}$ ，
∴（2 $\text{[math]}$ +3 $\text{[math]}$ ）（k $\text{[math]}$ - $\text{[math]}$ ）=0，
∴2k $\text{[math]}$ +（3k-2） $\text{[math]}$ -3 $\text{[math]}$ =0，
∵| $\text{[math]}$ |=1，| $\text{[math]}$ |=2， $\text{[math]}$ 与 $\text{[math]}$ 的夹角为60°，
∴2k+（3k-2）-12=0
∴5k=14
∴k= $\text{[math]}$
故选D．
点评：本题考查向量的垂直关系的充要条件，本题是一个基础题，题目中包含的向量之间的关系比较复杂，需要认真完成．

练习册系列答案

学考A加同步课时练系列答案

同步学考优化设计系列答案

品至教育期末100分系列答案

文轩图书暑假生活指导暑系列答案

启东专项听力训练系列答案

特优期末卷淘金系列系列答案

单元测试AB卷吉林出版集团有限责任公司系列答案

小学语文词语手册开明出版社系列答案

假期作业暑假乐园系列答案

英语听力与阅读能力训练系列答案

相关题目

已知-1＜2a＜0，A=1+a²，B=1-a²，C=

则A、B、C、D按从小到大的顺序排列起来是

8、已知1、2、3、4、7、9六个数．
（1）可以组成多少没有重复数字的五位数；
（2）其中有多少个是偶数；
（3）其中有多少个是3的倍数．

(xcosx+3a-b)dx=2a+6，f(t)=

(x3+ax+5a-b)dx为偶函数，则a+b=（　　）

已知-1＜a＜0，那么-a，-a³，a²的大小关系是（　　）

A．a²＞-a³＞-a

B．-a＞a²＞-a³

C．-a³＞-a＞a²

D．a²＞-a＞-a³

已知1＜a+b＜3且-1＜a-b＜1，则2a+b的取值范围是