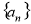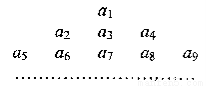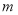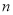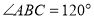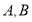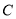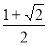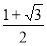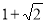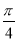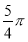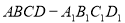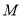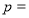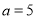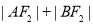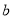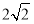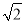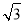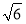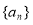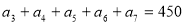题目内容
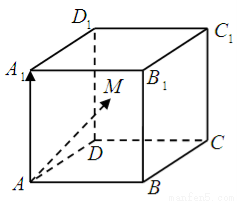
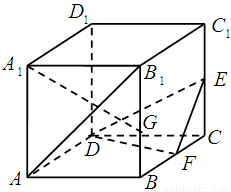
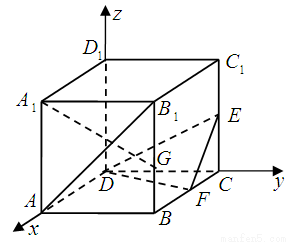
如图,已知正方体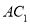 棱长为2,
棱长为2, 、
、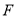 、
、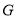 分别是
分别是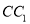 、
、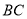 和
和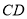 的中点.
的中点.
(1)证明: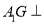 面
面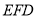 ;
;
(2)求二面角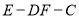 的余弦值.
的余弦值.
(1)证明详见解析;(2)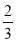 .
.
【解析】
试题分析:先以点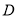 为原点建立空间直角坐标系,然后标明有效点的坐标,(1)写出有效向量
为原点建立空间直角坐标系,然后标明有效点的坐标,(1)写出有效向量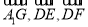 的坐标,利用向量的数量积为零即可证明
的坐标,利用向量的数量积为零即可证明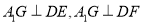 ,从而可得
,从而可得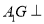 平面
平面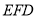 ;(2)易知
;(2)易知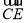 为平面
为平面 的法向量,先计算
的法向量,先计算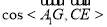 ,然后观察二面角
,然后观察二面角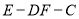 是锐角还是钝角,最终确定二面角
是锐角还是钝角,最终确定二面角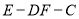 的余弦值.
的余弦值.
试题解析:以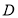 为原点建立如图空间直角坐标系,正方体棱长为2
为原点建立如图空间直角坐标系,正方体棱长为2
则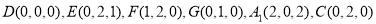 2分
2分
(1)则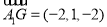 ,
,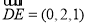
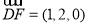 3分
3分
∵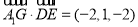
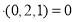
∴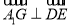 4分
4分
∵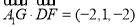
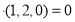
∴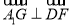 5分
5分
又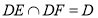 ,
,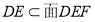 ,
,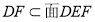 6分
6分
∴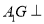 面
面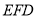 7分
7分
(2)由(1)知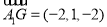 为面
为面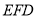 的法向量 8分
的法向量 8分
∵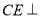 面
面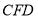 ,
,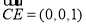 为面
为面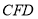 的法向量 9分
的法向量 9分
设 与
与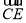 夹角为
夹角为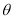 ,则
,则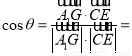
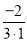
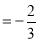 12分
12分
由图可知二面角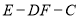 的平面角为
的平面角为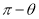
∴二面角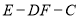 的余弦值为
的余弦值为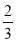 14分.
14分.
考点:1.空间向量在解决空间垂直上的应用;2.空间向量在解决空间角中的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目