题目内容
11.在平面直角坐标系xOy中,A(1,0),B(0,1),则点集{P|$\overrightarrow{OP}=m\overrightarrow{OA}+n\overrightarrow{OB}$},|m|+|n|=1,m,n∈R}所表示区域的周长是( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8 |
分析 根据条件容易求出点P的坐标(m,n),而|m|+|n|=1是由四条线段围成的正方形,可以画出该正方形,根据图形即可得出所围成区域的周长.
解答 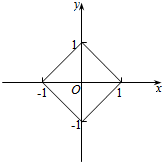 解:根据条件$\overrightarrow{OP}=(m,n)$,∴P(m,n);
解:根据条件$\overrightarrow{OP}=(m,n)$,∴P(m,n);
由|m|+|n|=1得:m>0,n>0时,m+n=1;m>0,n<0时,m-n=1;m<0,n>0时,-m+n=1;m<0,n<0时,-m-n=1;
∴|m|+|n|=1所围成的图形如图所示:
图形为正方形,周长为$4\sqrt{2}$.
故选B.
点评 考查起点在原点的向量坐标和向量终点坐标的关系,向量坐标的加法运算,直线的方程,弄清|m|+|n|=1表示的图形是求解本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1.设数列{an}是等差数列,a2=2,且a2、a3、a5成公比不为1的等比数列,那么{an}的前20项和为( )
| A. | 342 | B. | 380 | C. | 400 | D. | 420 |
19.若函数$f(x)=\frac{a}{x^2}$在(2,f(2))处的切线过点(1,2),则a=( )
| A. | 4 | B. | 7 | C. | 8 | D. | $\frac{8}{5}$ |
6.已知正项等比数列{an}的前n项和为Sn,若-3,S5,S10成等差数列,则S15-S10的最小值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |