题目内容
如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（ ）| A、∠B=∠C | B、∠ADC=∠AEB | C、BE=CD，AB=AC | D、AD：AC=AE：AB |
考点：相似三角形的判定
专题：几何证明
分析：由∠B=∠C或∠ADC=∠AEB或AD：AC=AE：AB，及∠A公用，都可以得到△ABE∽△ACD．即可得出．
解答：解：∠B=∠C或∠ADC=∠AEB或AD：AC=AE：AB，
又∠A公用，∴△ABE∽△ACD．
因此下列条件中不能使△ABE和△ACD相似的是：C．
故选：C．
又∠A公用，∴△ABE∽△ACD．
因此下列条件中不能使△ABE和△ACD相似的是：C．
故选：C．
点评：本题考查了相似三角形的判定条件，属于基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知f（x）=
x4-
x3+2x2+a在x=x1处取得极值2，则
dt=（ ）
| 1 |
| 4 |
| 4 |
| 3 |
| ∫ | 1 0 |
| a2-t2 |
A、π+
| ||||||||||||
| B、π | ||||||||||||
C、
| ||||||||||||
D、
|
i为虚数单位，复数z=1+i的模为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
在航天员进行的一项太空实验中，先后要实施6个程序，其中程序B和C都不与D相邻，则实验顺序的编排方法共有（ ）
| A、216种 | B、288种 | C、180种 | D、144种 |
（1-2x）6的展开式中x2项的系数是（ ）
| A、12 | B、54 | C、60 | D、160 |
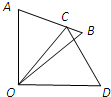如图，△COD是△AOB绕点O顺时针旋转36°后得到的图形，点C恰好在AB上，∠AOD的度数是90°，则∠B的度数是下列四边形中，四个顶点一定在同一个圆上的是（ ）
| A、平行四边行 | B、菱形 | C、矩形 | D、直角梯形 |