题目内容
已知在( -
- )n的展开式中,第6项为常数项.
)n的展开式中,第6项为常数项.(1)求n;
(2)求含x2项的系数;
(3)求展开式中所有的有理项.
【答案】分析:(1)由二项式定理,可得(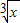 -
-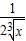 )n的展开式的通项,又由题意,可得当r=5时,x的指数为0,即
)n的展开式的通项,又由题意,可得当r=5时,x的指数为0,即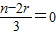 ,解可得n的值,
,解可得n的值,
(2)由(1)可得,其通项为Tr+1=(- )rC10r
)rC10r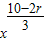 ,令x的指数为2,可得
,令x的指数为2,可得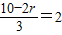 ,解可得r的值,将其代入通项即可得答案;
,解可得r的值,将其代入通项即可得答案;
(3)由(1)可得,其通项为Tr+1=(- )rC10r
)rC10r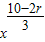 ,令x的指数为整数,可得当r=2,5,8时,是有理项,代入通项可得答案.
,令x的指数为整数,可得当r=2,5,8时,是有理项,代入通项可得答案.
解答:解:(1)根据题意,可得(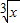 -
-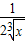 )n的展开式的通项为
)n的展开式的通项为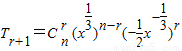 =
=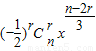 ,
,
又由第6项为常数项,则当r=5时,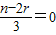 ,
,
即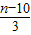 =0,解可得n=10,
=0,解可得n=10,
(2)由(1)可得,Tr+1=(- )rC10r
)rC10r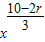 ,
,
令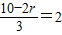 ,可得r=2,
,可得r=2,
所以含x2项的系数为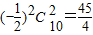 ,
,
(3)由(1)可得,Tr+1=(- )rC10r
)rC10r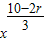 ,
,
若Tr+1为有理项,则有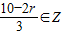 ,且0≤r≤10,
,且0≤r≤10,
分析可得当r=2,5,8时,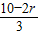 为整数,
为整数,
则展开式中的有理项分别为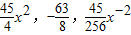 .
.
点评:本题考查二项式定理的应用,解题时要区分有理项与常数项,关键是根据二项式定理,写出其展开式的通项.
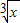 -
-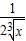 )n的展开式的通项,又由题意,可得当r=5时,x的指数为0,即
)n的展开式的通项,又由题意,可得当r=5时,x的指数为0,即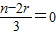 ,解可得n的值,
,解可得n的值,(2)由(1)可得,其通项为Tr+1=(-
 )rC10r
)rC10r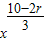 ,令x的指数为2,可得
,令x的指数为2,可得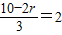 ,解可得r的值,将其代入通项即可得答案;
,解可得r的值,将其代入通项即可得答案;(3)由(1)可得,其通项为Tr+1=(-
 )rC10r
)rC10r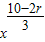 ,令x的指数为整数,可得当r=2,5,8时,是有理项,代入通项可得答案.
,令x的指数为整数,可得当r=2,5,8时,是有理项,代入通项可得答案.解答:解:(1)根据题意,可得(
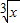 -
-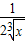 )n的展开式的通项为
)n的展开式的通项为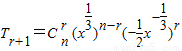 =
=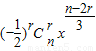 ,
,又由第6项为常数项,则当r=5时,
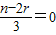 ,
,即
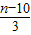 =0,解可得n=10,
=0,解可得n=10,(2)由(1)可得,Tr+1=(-
 )rC10r
)rC10r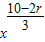 ,
,令
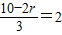 ,可得r=2,
,可得r=2,所以含x2项的系数为
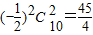 ,
,(3)由(1)可得,Tr+1=(-
 )rC10r
)rC10r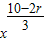 ,
,若Tr+1为有理项,则有
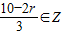 ,且0≤r≤10,
,且0≤r≤10,分析可得当r=2,5,8时,
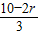 为整数,
为整数,则展开式中的有理项分别为
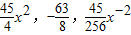 .
.点评:本题考查二项式定理的应用,解题时要区分有理项与常数项,关键是根据二项式定理,写出其展开式的通项.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目




