Question

（2012•衡阳模拟）某广场二雕塑造型结构如图所示，最上层是呈水平状态的圆环且圆心为O，其半径为2m，通过金厲杆BC，CA₁，CA₂，…，CA_n支撑在地面B处（BC垂直于水平面）．A₁，A₂，A₃，…，A_n是圆环上的n等分点，圆环所在的水平面距地面1Om，设金属杆CA₁，CA₂，…，CA_n所在直线与圆环所在水平面所成的角都为θ（圓环及金厲杆均不计粗细）
（1）当θ为60°且n=3时，求金厲杆BC，CA₁，CA₂，CA₃的总长？
（2）当θ变化，n一定时，为美观与安全起见，要求金属杆BC，CA₁，CA₂，…，CA_n的总长最短，此时θ的正弦值是多少？并由此说明n越大，C点的位置将会上移还是下移．

Answer 1

分析：（1）先画出图形，然后分别求出金厲杆BC，CA₁，CA₂，CA₃的长，从而可求出所求；
（2）设金属杆总长为ym，然后表示出y关于θ的函数，最后利用导数研究该函数的最值，即可求出所求．

解答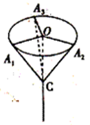：解：（1）当θ=60°且n=3时（如图），CA₁=CA₂=CA₃=4，OC=2

3

所以BC+CA₁+CA₂+CA₃=12+10-2

3

=22-2

3

（m）
（2）∵金属杆CA₁，CA₂，…，CA_n所在直线与圆环所在水平面所成的角都为θ
∴∠CA₁O=∠CA₂O=∠CA₃O=…=∠CA_nO=θ
CA₁=CA₂=CA₃=…=CA_n=

2

cosθ

，CO=2tanθ
设金属杆总长为ym，则
y=

2n

cosθ

+10-2tanθ=

2(n-sinθ)

cosθ

+10（0＜θ＜

π

2

）
y′=

2(nsinθ-1)

cos2θ

，当0＜sinθ＜

1

n

时，y′＜0，当

1

n

＜sinθ＜1时，y′＞0
所以当sinθ=

1

n

时，函数有极小值，也是最小值；
此时sinθ=

1

n

，n越大，sinθ越小，因为θ是锐角，所以θ也越小，因此C点上移了．

点评：本题主要考查了利用导数研究函数的最值，以及实际问题中导数的意义，同时考查了运算求解的能力和计算能力，属于中档题．