Question

选修4-1：几何证明选讲

如图，已经⊙O和⊙M相交于A、B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为弧BD中点，连结AG分别交⊙O、BD于点E、F，连结CE.

(Ⅰ) 求证：AG·EF=CE·GD；

(Ⅱ) 求证：

Answer 1

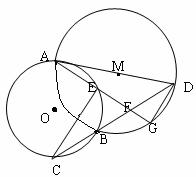
证明：（I）连结AB、AC，∵AD为⊙M的直径，

∴∠ABD=90°，∴AC为⊙O的直径，

∴∠CEF＝∠AGD=90°.     …………2分

∵∠DFC=∠CFE，∴ ∠ECF=∠GDF，

∵G为孤BD中点，∴∠DAG=∠GDF.…………4分

∵∠ECB=∠BAG，∴∠DAG=∠ECF，∴△CEF∽△AGD     …………5分

∴，   ∴AG·EF = CE·GD                               …………6分

（II）由（I）知∠DAG=∠GDF，∠G=∠G，

∴△DFG∽△AGD，   ∴DG²=AG·GF                                              …………8分

由（I）知，∴                                         …………10分