题目内容
(理科)已知椭圆C:
+
=1(a>b>0),过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
=λ
,
=μ
.求证:λ+μ为定值,并计算出该定值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
| AQ |
| QB |
| AE |
| EB |
分析:(1)根据椭圆过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形,建立方程组,求出几何量,从而写出椭圆的方程即可;
(2)易知直线l斜率存在,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再利用韦达定理及向量的坐标公式即可求得λ+μ值.
(2)易知直线l斜率存在,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再利用韦达定理及向量的坐标公式即可求得λ+μ值.
解答:(1)解:∵椭圆过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形
∴
,∴a=2,b=1,∴求椭圆的方程为
+y2=1;
(2)证明:由题意直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y0)
直线方程代入椭圆方程,消去y可得(1+4k2)x2+8k2x+4k2-4=0,∴△=48k2+16>0
x1+x2=-
,x1x2=
∵
=λ
,∴λ=
∵
=μ
,∴μ=
∴λ+μ=
+
=-
=
=0.
∴
|
| x2 |
| 4 |
(2)证明:由题意直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y0)
直线方程代入椭圆方程,消去y可得(1+4k2)x2+8k2x+4k2-4=0,∴△=48k2+16>0
x1+x2=-
| 8k2 |
| 1+4k2 |
| 4k2-4 |
| 1+4k2 |
∵
| AQ |
| QB |
| x1+1 |
| x2+1 |
∵
| AE |
| EB |
| x1+4 |
| x2+4 |
∴λ+μ=
| x1+1 |
| x2+1 |
| x1+4 |
| x2+4 |
| 2x1x2+5(x1+x2)+8 |
| (x2+1)(x2+4) |
2×
| ||||
| (x2+1)(x2+4) |
点评:本题主要考查椭圆的标准方程,考查直线与圆锥曲线的综合问题、向量在几何中的应用等基础知识,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
 )且方向向量为
)且方向向量为 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又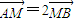 .
. )且方向向量为
)且方向向量为 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又 .
. )且方向向量为
)且方向向量为 的直线l交椭圆C于A、B两点,交x轴于M点,又
的直线l交椭圆C于A、B两点,交x轴于M点,又 .
.