题目内容
如图,BC为圆O的直径,A为圆O上一点,过点A作圆O的切线交BC的延长线于点P,AH⊥PB于H.
求证:PA·AH=PC·HB.


【证明】连AC,AB.
因BC为圆O的直径,故AC⊥AB.
又AH⊥PB,故AH2=CH·HB,即 .
.
因PA为圆O的切线,故∠PAC=∠B.
在Rt△ABC中,∠B+∠ACB=0°.
在Rt△ACH中,∠CAH+∠ACB=0°.
所以,∠HAC=∠B.
所以,∠PAC=∠CAH,
所以, ,即
,即 .
.
所以, ,即PA·AH=PC·HB.
,即PA·AH=PC·HB.



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 (r∈R)交于A,B两点,求以AB为直径的圆的极坐标方程.
(r∈R)交于A,B两点,求以AB为直径的圆的极坐标方程.
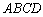 中,
中,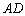 ∥
∥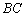 ,
,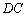 ⊥
⊥ ,
, ,若以
,若以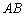 为直径的⊙
为直径的⊙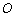 与
与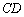 相切于点
相切于点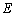 ,则
,则 等于( )
等于( )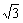 (B)
(B)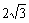
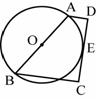

 内接于⊙
内接于⊙ ,
, 是⊙
是⊙ ,
, ,则
,则 _____,
_____, .
. 
 .
. 的解集;
的解集; 在R上恒成立,求实数a的取值范围.
在R上恒成立,求实数a的取值范围.