Question

已知圆C₁的方程为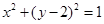，定直线l的方程为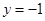．动圆C与圆C₁外切，且与直线l相切．

（Ⅰ）求动圆圆心C的轨迹M的方程；

（Ⅱ）直线与轨迹M相切于第一象限的点P，过点P作直线的垂线恰好经过点A（0，6），并交轨迹M于相异的两点P、Q，记为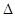POQ（O为坐标原点）的面积，求的值．

 

Answer 1

【答案】

（Ⅰ），即为动圆圆心C的轨迹M的方程；（II）。

【解析】

试题分析：（1）求解点的轨迹方程一般是先设出点的坐标，然后找到点所满足的关系式，进而得到结论。

（2）在第一问的基础上，设点P的坐标为，则，结合导数的几何意义，得到直线PQ的方程，让那后得到点的坐标，进而表示面积。

解:（Ⅰ）设动圆圆心C的坐标为，动圆半径为R，

则，且

    可得 ．．．．．．．．．．．．．3分

由于圆C₁在直线l的上方，所以动圆C的圆心C应该在直线l的上方，所以有，

，整理得，即为动圆圆心C的轨迹M的方程．．5分

（II）如图示，

设点P的坐标为，则，．．．．．．．．6分

，所以直线PQ的方程为．．．．．．．．．．．．．．．．．．．．．．．．8分

又,．点P在第一象限，，--9分

点P坐标为（4,2），直线PQ的方程为．--------------10分

联立得，解得或4，点Q的坐标为．所以---------12分

考点：本题主要考查直线与圆的位置关系以及圆与圆的位置关系的综合运用。

点评：解决该试题的关键是利用线与圆相切得到圆心到直线的距离等于圆的半径，利用两个圆相互外切，则说明圆心距等于半径之和得到结论。