题目内容
已知a>0,b>0,c>0,且ab=1,a2+b2+c2=4,则ab+bc+ac的最大值为
- A.
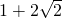
- B.

- C.3
- D.4
A
分析:由基本不等式a2+b2=4-c2≥2ab=2可求c的范围,然后由a+b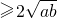 可求a+b的范围,从而可求ab+acbc的最大值
可求a+b的范围,从而可求ab+acbc的最大值
解答:∵a2+b2+c2=4,ab=1
∴a2+b2=4-c2≥2ab=2当且仅当a=b=1时取等号
∴c2≤2
∵c>0
∴0 ,
,
当c= 时,a=b=1
时,a=b=1
∴(a+b)c
则ab+bc+ac=1+(a+b)c
∴ab+acbc的最大值为1+2
故选A
点评:本题主要考查了基本不等式在求解最值中的应用,注意由已知分离出c是求解的关键
分析:由基本不等式a2+b2=4-c2≥2ab=2可求c的范围,然后由a+b
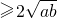 可求a+b的范围,从而可求ab+acbc的最大值
可求a+b的范围,从而可求ab+acbc的最大值解答:∵a2+b2+c2=4,ab=1
∴a2+b2=4-c2≥2ab=2当且仅当a=b=1时取等号
∴c2≤2
∵c>0
∴0
 ,
,当c=
 时,a=b=1
时,a=b=1∴(a+b)c

则ab+bc+ac=1+(a+b)c

∴ab+acbc的最大值为1+2

故选A
点评:本题主要考查了基本不等式在求解最值中的应用,注意由已知分离出c是求解的关键

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目