题目内容
在平面直角坐标系xOy中,已知点A(3,3),B(5,1),P(2,1),点M是直线OP上的一个动点.
(Ⅰ)求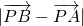 的值;
的值;
(Ⅱ)若四边形APBM是平行四边形,求点M的坐标;
(Ⅲ)求 的最小值.
的最小值.
解:(Ⅰ)∵点A(3,3),B(5,1),P(2,1),
∴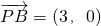 ,
,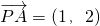 ,
,
∴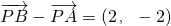 ,
,
∴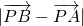 =
=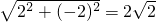 .
.
(Ⅱ)设点M(x,y).
∵四边形APBM是平行四边形,∴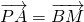 ,
,
∴(1,2)=(x-5,y-1),∴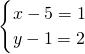 ,解得
,解得 .
.
∴M(6,3).
(Ⅲ)设点M(x,y).
则 .
.
由题意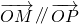 .
.
∴x-2y=0,即x=2y.
∴M(2y,y).
∴ =(3-2y,3-y)•(5-2y,1-y)
=(3-2y,3-y)•(5-2y,1-y)
=5y2-20y+18
=5(y-2)2-2.
∴当y=2时, 取得最小值-2,此时M(4,2).
取得最小值-2,此时M(4,2).
分析:(Ⅰ)利用向量的坐标运算和模的计算公式即可得出;
(Ⅱ)利用平行四边形的性质、向量共线的性质及其坐标坐标运算即可得出;
(Ⅲ)利用向量共线和二次函数的单调性即可得出.
点评:熟练掌握向量的坐标运算和模的计算公式、平行四边形的性质、向量共线的性质、向量共线定理和二次函数的单调性是解题的关键.
∴
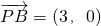 ,
,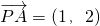 ,
,∴
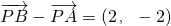 ,
,∴
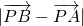 =
=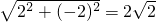 .
.(Ⅱ)设点M(x,y).
∵四边形APBM是平行四边形,∴
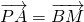 ,
,∴(1,2)=(x-5,y-1),∴
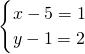 ,解得
,解得 .
.∴M(6,3).
(Ⅲ)设点M(x,y).
则
 .
.由题意
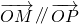 .
.∴x-2y=0,即x=2y.
∴M(2y,y).
∴
 =(3-2y,3-y)•(5-2y,1-y)
=(3-2y,3-y)•(5-2y,1-y)=5y2-20y+18
=5(y-2)2-2.
∴当y=2时,
 取得最小值-2,此时M(4,2).
取得最小值-2,此时M(4,2).分析:(Ⅰ)利用向量的坐标运算和模的计算公式即可得出;
(Ⅱ)利用平行四边形的性质、向量共线的性质及其坐标坐标运算即可得出;
(Ⅲ)利用向量共线和二次函数的单调性即可得出.
点评:熟练掌握向量的坐标运算和模的计算公式、平行四边形的性质、向量共线的性质、向量共线定理和二次函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.