题目内容

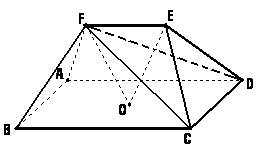（本题10分） 如图，在五面体EF-ABCD中，点O是矩形ABCD的对角线的交点，△CDE是等边三角形，棱              

（1）证明FO//平面CDE；

（2）设，证明EO⊥平面CDF.

（1）证明：取CD中点M，连结OM，在矩形ABCD中

，又，则。连结EM，

于是四边形EFOM为平行四边形     ∴ FO//EM

又 ∵ FO平面CDE，且EM平面CDE，∴ FO//平面CDE …………5分

（2）证明：连结FM，由（1）和已知条件，在等边中，CM=DM，EM⊥CD且。因此平行四边形EFOM为菱形，从而EO⊥FM

∵ CD⊥OM，CD⊥EM    ∴ CD⊥平面EOM，从而CD⊥EO

综上有，EO⊥FM，EO⊥CD而FMCD=M，所以平面CDF………………10分

练习册系列答案
相关题目

（本题10分）如图1，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AB＝4，AD＝CD＝2，M为线段AB的中点，将△ACD沿折起，使平面ACD⊥平面ABC，得到几何体D－ABC，如图2所示．

（Ⅰ）求证：BC⊥平面ACD；

（Ⅱ）求二面角A－CD－M的余弦值．

 

（本题10分）如图一边长为48cm的正方形铁皮，四角各截去一个大小相同的小正方形，然后折起，可以做成一个无盖长方体容器。所得容器的体积V（单位：)是关于截去的小正方形的边长x(单位：)的函数。⑴ 随着x的变化，容积V是如何变化的？

⑵ 截去的小正方形的边长为多少时，容器的容积最大？最大容积是多少？

 

 

 

（本题10分）如图，已知点A(2,3), B(4,1)，△ABC是以AB为底边的等腰三角形，点C在直线l：x－2y＋2＝0上

（Ⅰ）求AB边上的高CE所在直线的方程

（Ⅱ）求△ABC的面积

 

（附加题，本题10分）

如图所示，的图像下有一系列正三角形，求第n个正三角形的边长.

 

本题10分）如图，河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m., 为保证安全，要求通过的船顶部（设为平顶）与拱桥顶部在竖直方向上高度之差至少要有0.5m.

  （1）一条船船顶部宽4m，要使这艘船安全通过，则船在水面以上部分高不能超过多少米？

  （2）近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽m，在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网