Question

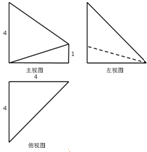（2013•济南一模）一个几何体的三视图如图所示，则它的体积为（　　）

• A．

  20

  3

• B．

  40

  3

• C．20
• D．40

Answer 1

分析：三视图的俯视图是等腰直角三角形，结合主视图和左视图得到原几何体，该几何体是以直角梯形ABEF为底面，以CA为高的四棱锥的侧放图，所以其体积为

1

3

×SABEF×AC．

解答：解：由俯视图看出原几何体的底面是边长为4的等腰直角三角形，
结合主视图和左视图看出几何体有两条棱和底面垂直，所以，
由三视图还原原几何体如图，

其中ABC为等腰直角三角形，AB=AC=4，∠BAC=90°，
FA⊥底面ABC，FA=4，EB⊥底面ABC，EB=1，
四边形ABEF为直角梯形，
所以该几何体的体积为VC-ABEF=

1

3

×SABEF×AC=

1

3

×

1

2

×(1+4)×4×4=

40

3

．
故选B．

点评：该题考查了由几何体的三视图求几何体的体积，解答的关键是正确还原原几何体，还原的方法是先看俯视图，结合主视图和左视图，此题是基础题．