题目内容
已知f(x)=x2﹣alnx在(1,2]上是增函数,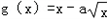 在(0,1)上是减函数.
在(0,1)上是减函数.
(1)求a的值;
(2)设函数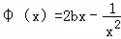 在(0,1]上是增函数,且对于(0,1]内的任意两个变量s,t,恒有f(s)≥φ(t)成立,求实数b的取值范围;
在(0,1]上是增函数,且对于(0,1]内的任意两个变量s,t,恒有f(s)≥φ(t)成立,求实数b的取值范围;
(3)设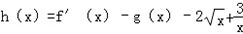 ,求证:[h(x)]n+2≥h(xn)+2n(n∈N*).
,求证:[h(x)]n+2≥h(xn)+2n(n∈N*).
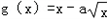 在(0,1)上是减函数.
在(0,1)上是减函数.(1)求a的值;
(2)设函数
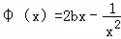 在(0,1]上是增函数,且对于(0,1]内的任意两个变量s,t,恒有f(s)≥φ(t)成立,求实数b的取值范围;
在(0,1]上是增函数,且对于(0,1]内的任意两个变量s,t,恒有f(s)≥φ(t)成立,求实数b的取值范围;(3)设
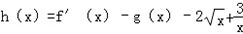 ,求证:[h(x)]n+2≥h(xn)+2n(n∈N*).
,求证:[h(x)]n+2≥h(xn)+2n(n∈N*).解:(1) ,依题意,当x∈(1,2]时,f'(x)≥0恒成立,
,依题意,当x∈(1,2]时,f'(x)≥0恒成立,
即a≤(2x2)min a≤2.
a≤2. ,当x∈(0,1)时,g'(x)≤0恒成立,即a≥2,
,当x∈(0,1)时,g'(x)≤0恒成立,即a≥2,
所以a=2.
(2) ,
,
所以f(x)在(0,1]上是减函数,最小值是f(1)=1. 在(0,1]上是增函数,即
在(0,1]上是增函数,即 恒成立,
恒成立,
得b≥﹣1,且φ(x)的最大值是φ(1)=2b﹣1,
由已知得1≥2b﹣1 b≤1,
b≤1,
所以b的取值范围是[﹣1,1].
(3) ,n=1时不等式左右相等,得证;
,n=1时不等式左右相等,得证;
n≥2时,
= ,
,
所以,[h(x)]n+2≥h(xn)+2n(n∈N*)成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目