题目内容
在极坐标系
 中,曲线
中,曲线 与ρcosθ=-1 的交点的极坐标为________
与ρcosθ=-1 的交点的极坐标为________

解析试题分析:解:将ρ=2sinθ代入ρcosθ=-1,得2sinθcosθ=-1,∴sin2θ=-1.
∵0≤θ≤2π,及sinθ≥0,cosθ≤0,∴ ≤θ≤π,∴π≤2θ≤2π,∴2θ=
≤θ≤π,∴π≤2θ≤2π,∴2θ= ,∴θ=
,∴θ= .将θ=
.将θ= 代入ρ=2sinθ,得ρ=2×sin
代入ρ=2sinθ,得ρ=2×sin =
= .故曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
.故曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为 .故答案为
.故答案为 。
。
考点:极坐标系中的曲线与曲线的交点
点评:本题考查极坐标系中的曲线与曲线的交点的极坐标,可直接代入计算出,亦可先化为普通方程求出其交点坐标,然后再化为极坐标

练习册系列答案
相关题目
 作圆
作圆 的切线,则切线的极坐标方程是 .
的切线,则切线的极坐标方程是 .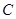 :
: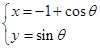
 为参数)和直线:
为参数)和直线: (为参数), 则曲线
(为参数), 则曲线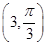 、
、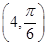 ,则
,则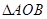 (其中O为极点)的面积为
(其中O为极点)的面积为 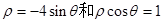 相交于点A、B,则|AB|= 。
相交于点A、B,则|AB|= 。 与
与 的两个圆的圆心距离为_________。
的两个圆的圆心距离为_________。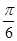 和sinθ=
和sinθ= ; ②θ=
; ②θ=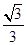 ; ③ρ2-9=0和ρ= 3;
; ③ρ2-9=0和ρ= 3; 和
和 . 其中表示相同曲线的组数为 .
. 其中表示相同曲线的组数为 . 的圆心,且垂直于极轴的直线的极坐标方程为 。
的圆心,且垂直于极轴的直线的极坐标方程为 。 且与极轴垂直的直线交曲线
且与极轴垂直的直线交曲线 于A、B两点,则
于A、B两点,则 ______
______  _.
_. 