题目内容
已知数列{an}是各项均为正数的等差数列,则有
- A.
 <
<
- B.
 ≤
≤
- C.
 >
>
- D.
 ≥
≥
B
分析:利用等差数列的通项公式,分别求出a4a8 和a62,比较它们的大小,得到 a4a8≤a62,从而得出答案.
解答:∵数列{an}是各项均为正数的等差数列,∴d≥0
∵a4a8=(a1+3d)(a1+7d)=a12+10a1d+21d2,
a62=(a1+5d)2═a12+10a1d+25d2,a62-a4a8=4d2≥0,
∴a4a8≤a62,∴ ≤
≤ ,
,
故选B.
点评:本题考查等差数列的性质,等差数列的通项公式的应用,得到 a4a8≤a62 是解题的关键.
分析:利用等差数列的通项公式,分别求出a4a8 和a62,比较它们的大小,得到 a4a8≤a62,从而得出答案.
解答:∵数列{an}是各项均为正数的等差数列,∴d≥0
∵a4a8=(a1+3d)(a1+7d)=a12+10a1d+21d2,
a62=(a1+5d)2═a12+10a1d+25d2,a62-a4a8=4d2≥0,
∴a4a8≤a62,∴
 ≤
≤ ,
,故选B.
点评:本题考查等差数列的性质,等差数列的通项公式的应用,得到 a4a8≤a62 是解题的关键.

练习册系列答案
相关题目
 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足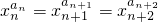 (n∈N*).
(n∈N*).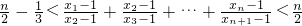 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.