题目内容
△ABC中，点D在边AB上，CD平分∠ACB，若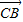
=a，
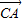=b，|a|=1，|b|=2，则
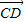=（ ）A．
a+
bB．
a+
bC．
a+
bD．
a+
b
【答案】分析：由△ABC中，点D在边AB上，CD平分∠ACB，根据三角形内角平分线定理，我们易得到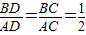
，我们将
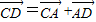后，将各向量用
，
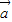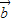表示，即可得到答案．
解答：解：∵CD为角平分线，
∴
，
∵
，
∴
，
∴
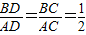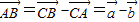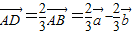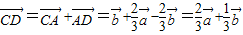
故选B
点评：本题考查了平面向量的基础知识，解答的核心是三角形内角平分线定理，即若AD为三角形ABC的内角A的角平分线，则AB：AC=AD：CD
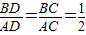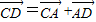，我们将后，将各向量用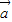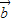，表示，即可得到答案．解答：解：∵CD为角平分线，
∴
，∵
，∴
，∴
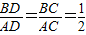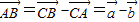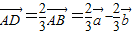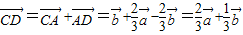
故选B
点评：本题考查了平面向量的基础知识，解答的核心是三角形内角平分线定理，即若AD为三角形ABC的内角A的角平分线，则AB：AC=AD：CD
练习册系列答案
名题金卷系列答案
相关题目
△ABC中，点D在边AB上，CD平分∠ACB，若
=
，
=
，|
|=1，|
|=2，则
=（ ）
| CB |
| a |
| CA |
| b |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
= a , 
= b , 
= 1 ，
= 2, 则
=
a + 
b （B）
a +
b （D）
= a , 
= b , 
= 1 ，
= 2, 则
=
a + 
b （B）
a +
b （D）
＝a，C
＝b，|a|＝1，|b|＝2，则C
＝( )
a＋
b B. 
a＋
b D. 
＝a，
＝b，|a|＝1，|b|＝2，则
等于( )
a＋
b B. 
a＋
b D.