题目内容
已知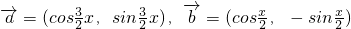 ,若
,若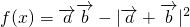 .
.
(I)求函数f(x)的单调减区间;
(II)若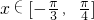 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.
解:(I)因为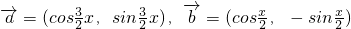
所以,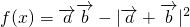 =
=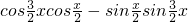 -
-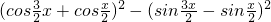
=cos2x-2-2cos2x=-2-cos2x
由2kπ-π≤2x≤2kπ k∈Z 可得 k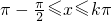 k∈Z.
k∈Z.
所以函数的单调减区间为: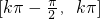 k∈Z.
k∈Z.
(II)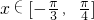 所以
所以  ,cos2x∈
,cos2x∈ ,
,
所以:-2-cos2x∈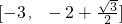 ,
,
所以函数的最大值为: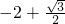 ;最小值为:-3.
;最小值为:-3.
分析:(I)通过向量的数量积与向量的模,求出函数的表达式互为一个角的一个三角函数的形式,借助余弦函数的单调增区间,求出函数f(x)的单调减区间;
(II)若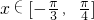 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.
点评:本题是中档题,以向量的数量积,向量的模为载体,考查三角函数的化简求值,三角函数的单调减区间的求法,闭区间上的最值问题,考查计算能力.
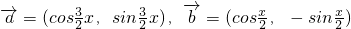
所以,
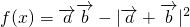 =
=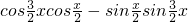 -
-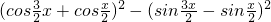
=cos2x-2-2cos2x=-2-cos2x
由2kπ-π≤2x≤2kπ k∈Z 可得 k
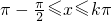 k∈Z.
k∈Z.所以函数的单调减区间为:
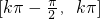 k∈Z.
k∈Z.(II)
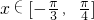 所以
所以  ,cos2x∈
,cos2x∈ ,
,所以:-2-cos2x∈
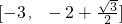 ,
,所以函数的最大值为:
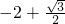 ;最小值为:-3.
;最小值为:-3.分析:(I)通过向量的数量积与向量的模,求出函数的表达式互为一个角的一个三角函数的形式,借助余弦函数的单调增区间,求出函数f(x)的单调减区间;
(II)若
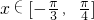 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.点评:本题是中档题,以向量的数量积,向量的模为载体,考查三角函数的化简求值,三角函数的单调减区间的求法,闭区间上的最值问题,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.