题目内容
(本题满分10分)
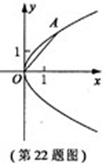
在平面直角坐标系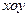 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在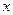 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点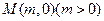 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为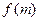 ,求
,求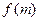 关于
关于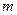 的表达式。
的表达式。

在平面直角坐标系
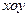 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在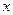 轴上。
轴上。(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点
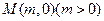 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为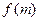 ,求
,求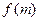 关于
关于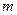 的表达式。
的表达式。
练习册系列答案
相关题目





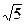 .
.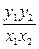 等于( )
等于( ) 一光源在点M(
一光源在点M( ,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
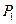 ,
,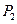 ,…,
,…,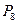 是抛物线
是抛物线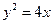 上的点,它们的横坐标依次为
上的点,它们的横坐标依次为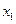 ,
,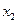 ,…,
,…,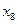 ,F是抛物线的焦点,若
,F是抛物线的焦点,若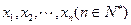 成等差数列且
成等差数列且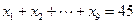 ,则
,则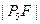 =( ).
=( ).


 的焦点坐标、离心率和准线方程。
的焦点坐标、离心率和准线方程。 的
的 焦点坐标是 ( )
焦点坐标是 ( ) D.(-4,0)
D.(-4,0)