Question

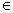(2004江苏，12)设函数，区间M=[a，b](a＜b)，集合N={y|y=f(x)，xM}，则使M=N成立的实数对(a，b)有

[　　]

A．0个	B．1个
C．2个	D．无数多个

Answer 1

答案：A
解析：

∵xM，M=[a，b]，则f(x)的定义域为[a，b]，N={y|y=f(x)，xM}，则f(x)的值域为N=M=[a，b]． 又∵是减函数． ∴f(x)在[a，b]上是减函数．则N=[f(b)，f(a)]=[a，b]＝M， 即解之得a=b=0，这与a＜b矛盾. ∴实数对(a，b)不存在．故选A．