题目内容
已知函数f(x)=sin(ωx+ψ)(ω>0,0≤ψ≤π)上R上的偶函数,其图象关于点M(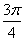 ,0)对称,且在区间
,0)对称,且在区间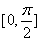 上是单调函数,求ψ和ω的值。
上是单调函数,求ψ和ω的值。
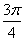 ,0)对称,且在区间
,0)对称,且在区间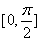 上是单调函数,求ψ和ω的值。
上是单调函数,求ψ和ω的值。 解:由f(x)是偶函数,得f(-x)=f(x),即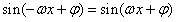 ,
,
所以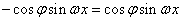 ,
,
对任意x都成立,且ω>0,所以得cosψ=0,
依题设0≤ψ≤π,所以解得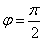 ,
,
由f(x)的图像关于点M对称,得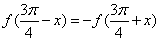 ,
,
取x=0,得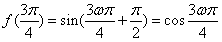 ,
,
∴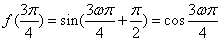 ,
,
∴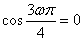 ,
,
又ω>0,得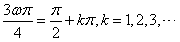 ,
,
∴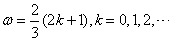 ,
,
当k=0时,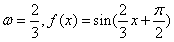 在
在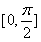 上是减函数;
上是减函数;
当k=1时,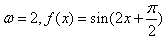 在
在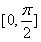 上是减函数;
上是减函数;
当k≥0时,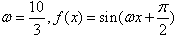 在
在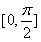 上不是单调函数,
上不是单调函数,
所以,综合得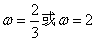 。
。
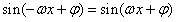 ,
,所以
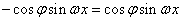 ,
,对任意x都成立,且ω>0,所以得cosψ=0,
依题设0≤ψ≤π,所以解得
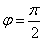 ,
,由f(x)的图像关于点M对称,得
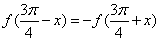 ,
,取x=0,得
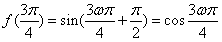 ,
,∴
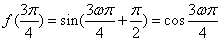 ,
,∴
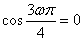 ,
,又ω>0,得
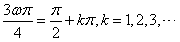 ,
,∴
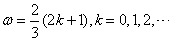 ,
,当k=0时,
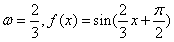 在
在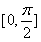 上是减函数;
上是减函数;当k=1时,
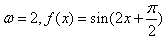 在
在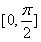 上是减函数;
上是减函数;当k≥0时,
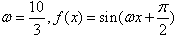 在
在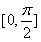 上不是单调函数,
上不是单调函数,所以,综合得
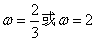 。
。 
练习册系列答案
相关题目
 将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表:
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表: