Question

已知四面体的4条棱的长为2，2条棱的长为3，求它的体积．

Answer 1

分析：由给出的四面体的4条棱的长为2，2条棱的长为3，分两类情况作出图形，经求解可知，当两条长为3的棱异面时，四面体不存在，当两条长为3的棱共面时，把要求的四面体的体积转化为两个三棱锥的体积和，求出共同的底面积后代入棱锥体积公式求解．

解答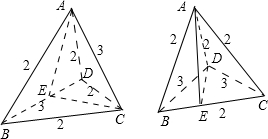：解：根据分析可知满足题目条件的四面体有两种情况，也就是棱长为3的棱共面和异面
（1）当棱长为3的棱异面时，四面体的图形如左图，
取BD的中点E，连接AE，CE，则AE⊥BD，CE⊥BD．
则VA-BCD=VB-AEC+VD-AEC=

1

3

S△AEC•BE+

1

3

S△AEC•DE
=

1

3

S△AEC•(BE+DE)=

1

3

S△AEC•BD
在直角三角形AEB和直角三角形CEB中，求得|CE|=|AE|=

7

2

，
∵|CE|+|AE|=

7

2

+

7

2

=

7

＜3=|AC|，所以三角形AEC并不存在，即这种情况的三棱锥也不存在．
（2）当棱长为3的棱共面时，四面体的图形如右图，
取BC中点E，则AE⊥BC，DE⊥BC，
则VA-BCD=VB-AED+VC-AED=

1

3

S△AED•BE+

1

3

S△AED•CE
=

1

3

S△AED•(BE+CE)=

1

3

S△AED•BC
在三角形AED中，AE=

3

，DE=2

2

，AD=2，
所以cos∠DAE=

22+( 3 )2-(2 2 )2

2×2× 3

=-

3

12

．
sin∠DAE=

1-(- 3 12 )2

=

141

12

．
所以S△AED=

1

2

AD•AE•sin∠DAE=

1

2

×2×

3

×

141

12

=

47

4

．
所以，VA-BCD=

1

3

S△AED•BC=

1

3

×

47

4

×2=

47

6

．

点评：本题考查了棱锥的体积，考查了分类讨论的数学思想和数学转化思想，能够正确排除两条长为3的棱异面时的情况是解答该题的关键．此题是中档题