题目内容
设M={x|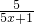 ≥1},N={x|x2-x<0},则
≥1},N={x|x2-x<0},则
- A.M∩N=φ
- B.M∩N=M
- C.M∪N=M
- D.M∪N=R
B
分析:M、N分别是分式不等式和二次不等式的解集,分别解出再求交集或并集即得.
解答:由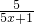 ≥1得
≥1得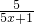 -1≥0,解得
-1≥0,解得 <x≤
<x≤ ;
;
由x2-x<0得0<x<1.
∴集合M={x| <x≤
<x≤ },N={x|0<x<1},
},N={x|0<x<1},
∴M∩N=M,
故选B.
点评:本题考查二次不等式和分式不等式的解集,以及集合的基本运算,较简单.
分析:M、N分别是分式不等式和二次不等式的解集,分别解出再求交集或并集即得.
解答:由
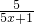 ≥1得
≥1得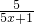 -1≥0,解得
-1≥0,解得 <x≤
<x≤ ;
;由x2-x<0得0<x<1.
∴集合M={x|
 <x≤
<x≤ },N={x|0<x<1},
},N={x|0<x<1},∴M∩N=M,
故选B.
点评:本题考查二次不等式和分式不等式的解集,以及集合的基本运算,较简单.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
