题目内容
双曲线C: 上一点
上一点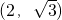 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.
(1)求双曲线的方程;
(2)设F1,F2是双曲线的左右焦点,P是双曲线上的点,若|PF1|+|PF2|=6,求△PF1F2的面积;
(3)过(-2,0)作直线l交双曲线C于A,B两点,若 ,是否存在这样的直线l,使OAPB为矩形?若存在,求出l的方程,若不存在,说明理由.
,是否存在这样的直线l,使OAPB为矩形?若存在,求出l的方程,若不存在,说明理由.
解:(1)∵双曲线C: 上一点
上一点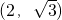 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.
∴a=1,双曲线方程为 ,
,
把点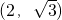 2,
2, )代入,得b=1.
)代入,得b=1.
∴双曲线方程为:x2-y2=1.
(2)设P在第一象限,则 ,
,
解得|PF1|=4,|PF2|=2,
∴ ,
,
∴ ,
,
∴△PF1F2的面积S= .
.
(3)若直线斜率存在,设为y=k(x+2),代入x2-y2=1,
得(1-(1-k2)x2-4k2x-4k2-1=0(k≠±1),
若平行四边形OAPB为矩形,则OA⊥OB,
∴x1x2+y1y2=0,
∴ 无解.
无解.
若直线垂直x轴,则A(-2, ),B(-2,
),B(-2, )不满足.
)不满足.
故不存在直线l,使OAPB为矩形.
分析:(1)由双曲线C: 上一点
上一点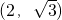 到左,右两焦点距离的差为2.知a=1,把点
到左,右两焦点距离的差为2.知a=1,把点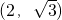 2,
2, )代入,得b=1.由此能求出双曲线方程.
)代入,得b=1.由此能求出双曲线方程.
(2)设P在第一象限,则 ,解得|PF1|=4,|PF2|=2,由此能求了△PF1F2的面积.
,解得|PF1|=4,|PF2|=2,由此能求了△PF1F2的面积.
(3)若直线斜率存在,设为y=k(x+2),代入x2-y2=1,得(1-(1-k2)x2-4k2x-4k2-1=0(k≠±1),若平行四边形OAPB为矩形,则OA⊥OB,由此能求出不存在直线l,使OAPB为矩形.
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 上一点
上一点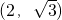 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.∴a=1,双曲线方程为
 ,
,把点
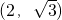 2,
2, )代入,得b=1.
)代入,得b=1.∴双曲线方程为:x2-y2=1.
(2)设P在第一象限,则
 ,
,解得|PF1|=4,|PF2|=2,
∴
 ,
,∴
 ,
,∴△PF1F2的面积S=
 .
.(3)若直线斜率存在,设为y=k(x+2),代入x2-y2=1,
得(1-(1-k2)x2-4k2x-4k2-1=0(k≠±1),
若平行四边形OAPB为矩形,则OA⊥OB,
∴x1x2+y1y2=0,
∴
 无解.
无解.若直线垂直x轴,则A(-2,
 ),B(-2,
),B(-2, )不满足.
)不满足.故不存在直线l,使OAPB为矩形.
分析:(1)由双曲线C:
 上一点
上一点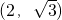 到左,右两焦点距离的差为2.知a=1,把点
到左,右两焦点距离的差为2.知a=1,把点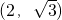 2,
2, )代入,得b=1.由此能求出双曲线方程.
)代入,得b=1.由此能求出双曲线方程.(2)设P在第一象限,则
 ,解得|PF1|=4,|PF2|=2,由此能求了△PF1F2的面积.
,解得|PF1|=4,|PF2|=2,由此能求了△PF1F2的面积.(3)若直线斜率存在,设为y=k(x+2),代入x2-y2=1,得(1-(1-k2)x2-4k2x-4k2-1=0(k≠±1),若平行四边形OAPB为矩形,则OA⊥OB,由此能求出不存在直线l,使OAPB为矩形.
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是
左支上一点到左焦点的距离是7,则该点到双曲线右焦点的距离是 上一点
上一点 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2. ,是否存在这样的直线l,使OAPB为矩形?若存在,求出l的方程,若不存在,说明理由.
,是否存在这样的直线l,使OAPB为矩形?若存在,求出l的方程,若不存在,说明理由.