题目内容
已知焦点在x轴上的椭圆的离心率为
，它的长轴长等于圆C：x2+y2-2x-15=0的半径，则椭圆的标准方程是
- A.
+
=1 - B.
+
=1 - C.+y2=1
- D.+
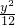=1
A
分析：利用配方化简x2+y2-2x-15=0得到圆的半径为4，所以椭圆的长轴为4，根据离心率求出c，根据勾股定理求出b得到椭圆的解析式即可．
解答：∵x2+y2-2x-15=0，
∴（x-1）2+y2=16，
∴r=4=2a，
∴a=2，
∵e=，∴c=1，∴b2=3．
故选A
点评：考查学生会根据条件求圆标准方程，以及灵活运用椭圆简单性质解决数学问题的能力．
分析：利用配方化简x2+y2-2x-15=0得到圆的半径为4，所以椭圆的长轴为4，根据离心率求出c，根据勾股定理求出b得到椭圆的解析式即可．
解答：∵x2+y2-2x-15=0，
∴（x-1）2+y2=16，
∴r=4=2a，
∴a=2，
∵e=
，∴c=1，∴b2=3．故选A
点评：考查学生会根据条件求圆标准方程，以及灵活运用椭圆简单性质解决数学问题的能力．
练习册系列答案
相关题目
＋
＝1的焦点为F1、F2，能否在x轴下方的椭圆弧上找到一点M，使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项？若存在，求出M点坐标；若不存在，说明理由．
的椭圆，使两端点A、B恰好重合于椭圆的一个短轴端点，如图2；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在x轴上，已知此时点A的坐标为（0，1），如图3，在图形变化过程中，图1中线段AM的长度对应于图3中的椭圆弧ADM的长度．图3中直线AM与直线y=-2交于点N（n，-2），则与实数m对应的实数就是n，记作f（m）=n，
；②函数f（m）是奇函数；③函数f（m）在（0，k）上单调递增；④函数f（m）的图象关于点
对称；⑤函数
时AM过椭圆的右焦点．其中所有的真命题是（ ）
和椭圆弧
