题目内容
(本题 10分)定义在R上的函数
10分)定义在R上的函数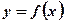 ,对任意的
,对任意的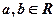 ,满足
,满足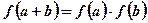 ,当
,当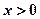 时,有
时,有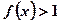 ,其中
,其中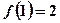 .
.
(1)求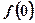 的值;
的值;
(2)求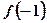 的值并判断该函数的奇偶性;
的值并判断该函数的奇偶性;
(3)求不等式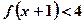 的解集.
的解集.
 10分)定义在R上的函数
10分)定义在R上的函数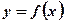 ,对任意的
,对任意的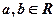 ,满足
,满足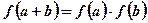 ,当
,当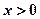 时,有
时,有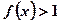 ,其中
,其中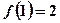 .
.
(1)求
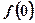 的值;
的值;(2)求
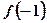 的值并判断该函数的奇偶性;
的值并判断该函数的奇偶性;(3)求不等式
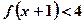 的解集.
的解集.(1)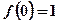
(2)f(-1)=,f(1)=2,所以原函数既不是奇函数,也不是偶函数.
(3)原不等式的解集为(-∞,1).
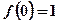
(2)f(-1)=,f(1)=2,所以原函数既不是奇函数,也不是偶函数.
(3)原不等式的解集为(-∞,1).
(1)因为对任意的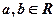 ,满足
,满足
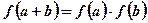 ,
,
所以令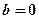 ,则
,则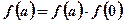 ,
,
当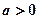 时,有
时,有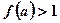 ,所以
,所以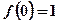 .
.
(2)f(-1)=,f(1)=2,所以原函数既不是奇函数,也不是偶函数.
(3)证明原函数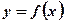 在R上是单调递增函数.
在R上是单调递增函数.
利用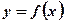 为单调递增函数,解得原不等式的解集为(-∞,1).
为单调递增函数,解得原不等式的解集为(-∞,1).
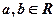 ,满足
,满足
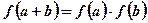 ,
,所以令
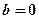 ,则
,则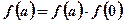 ,
,当
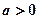 时,有
时,有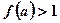 ,所以
,所以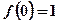 .
. (2)f(-1)=,f(1)=2,所以原函数既不是奇函数,也不是偶函数.
(3)证明原函数
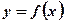 在R上是单调递增函数.
在R上是单调递增函数. 利用
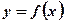 为单调递增函数,解得原不等式的解集为(-∞,1).
为单调递增函数,解得原不等式的解集为(-∞,1).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有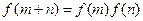 且当
且当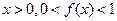
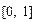 ,
, 且同时满足:①f(1)=3;②
且同时满足:①f(1)=3;②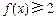 对一切
对一切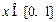 恒成立;③若
恒成立;③若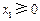 ,
,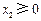 ,
,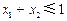 ,则
,则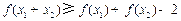 .
. 和最小值;
和最小值;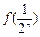 与
与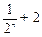
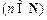 的大小;
的大小;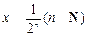 时,有
时,有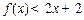 ,由此他提出猜想:对一切
,由此他提出猜想:对一切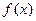 的定义域为
的定义域为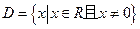 ,且满足对于任意的实数
,且满足对于任意的实数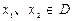 ,有
,有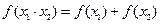 .
.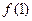 的值; (Ⅱ)判断
的值; (Ⅱ)判断 II)若
II)若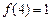 ,且
,且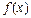 在
在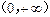 上是增函数,解关于
上是增函数,解关于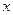 的不等式
的不等式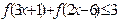 .
.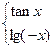
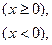 则f(
则f(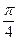 +2)· f(-98)的值为________。
+2)· f(-98)的值为________。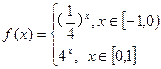 ,则
,则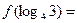 ( )
( ) 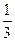
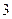
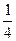
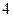
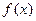 满足
满足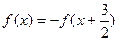 ,且
,且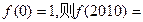 。
。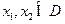 ,当
,当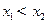 时,都有
时,都有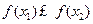 ,则称函数
,则称函数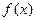 在D上为非减函数. 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件:1
在D上为非减函数. 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件:1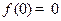 ; 2
; 2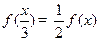 ; 3
; 3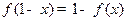 .
.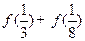 等于( )
等于( ) 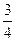
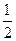
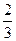
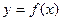 满足
满足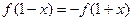 ,且对于任意
,且对于任意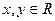 ,
, 不等式
不等式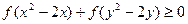 恒成立,则当
恒成立,则当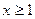 时,
时,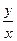 的取值范围为 ;
的取值范围为 ;