题目内容
下列4个命题:
①已知 是单位向量,|
是单位向量,| +
+ |=|
|=| -2
-2 |,则
|,则 在
在 方向上的投影为
方向上的投影为 ;
;
②关于x的不等式a 恒成立,则a的取值范围是a
恒成立,则a的取值范围是a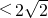 ;
;
③函数f(x)=alog2|x|+x+b为奇函数的充要条件是a+b=0;
④将函数y=sin(2x+ )图象向右平移
)图象向右平移 个单位,得到函数y=sin2x的图象
个单位,得到函数y=sin2x的图象
其中正确的命题序号是________(填出所有正确命题的序号).
①
分析:化简①由已知化简可得 =
=
 ,而要求的等于|
,而要求的等于| |cos<
|cos< ,
, >,代入化简,即可判断正误.②不等式恒成立转化成函数的最值进行判断出;③通过举反例对③进行判断;④利用函数图象的平移判断正误即可;
>,代入化简,即可判断正误.②不等式恒成立转化成函数的最值进行判断出;③通过举反例对③进行判断;④利用函数图象的平移判断正误即可;
解答:对于①,∵| +
+ |=|
|=| -2
-2 |,∴(|
|,∴(| +
+ |)2=(|
|)2=(| -2
-2 |)2,
|)2,
展开化简可得: =
=
 ,
,
故 在
在 方向上的投影等于|
方向上的投影等于| |cos<
|cos< ,
, >=
>= =
= ,所以①正确.
,所以①正确.
对于②∵0≤sin2x≤1,令sin2x=t,
∴ =t+
=t+ ,则令f(t)=t+
,则令f(t)=t+ ,t∈[0,1],
,t∈[0,1],
根据其图象可知,当x> 时,f(t)为递增的,当0<x≤
时,f(t)为递增的,当0<x≤ 时,f(t)为递减的,
时,f(t)为递减的,
∵t∈[0,1],∴f(t)≥f(1)=1+2=3,∴ ≥3
≥3
∵a< 恒成立时,只要a小于
恒成立时,只要a小于 的最小值即可,所以a<3,所以②不正确.
的最小值即可,所以a<3,所以②不正确.
对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数,故③错,
对于④将函数y=sin(2x+ )图象向右平移
)图象向右平移 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x- )的图象,所以④不正确.
)的图象,所以④不正确.
正确只有①.
故答案为:①.
点评:本题考查向量的投影,转化为向量的数量积和模长来运算是解决问题的关键,不等式恒成立问题,考查的知识点比较多,属基础题.
分析:化简①由已知化简可得
 =
=
 ,而要求的等于|
,而要求的等于| |cos<
|cos< ,
, >,代入化简,即可判断正误.②不等式恒成立转化成函数的最值进行判断出;③通过举反例对③进行判断;④利用函数图象的平移判断正误即可;
>,代入化简,即可判断正误.②不等式恒成立转化成函数的最值进行判断出;③通过举反例对③进行判断;④利用函数图象的平移判断正误即可;解答:对于①,∵|
 +
+ |=|
|=| -2
-2 |,∴(|
|,∴(| +
+ |)2=(|
|)2=(| -2
-2 |)2,
|)2,展开化简可得:
 =
=
 ,
,故
 在
在 方向上的投影等于|
方向上的投影等于| |cos<
|cos< ,
, >=
>= =
= ,所以①正确.
,所以①正确.对于②∵0≤sin2x≤1,令sin2x=t,
∴
 =t+
=t+ ,则令f(t)=t+
,则令f(t)=t+ ,t∈[0,1],
,t∈[0,1],根据其图象可知,当x>
 时,f(t)为递增的,当0<x≤
时,f(t)为递增的,当0<x≤ 时,f(t)为递减的,
时,f(t)为递减的,∵t∈[0,1],∴f(t)≥f(1)=1+2=3,∴
 ≥3
≥3∵a<
 恒成立时,只要a小于
恒成立时,只要a小于 的最小值即可,所以a<3,所以②不正确.
的最小值即可,所以a<3,所以②不正确.对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数,故③错,
对于④将函数y=sin(2x+
 )图象向右平移
)图象向右平移 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x- )的图象,所以④不正确.
)的图象,所以④不正确.正确只有①.
故答案为:①.
点评:本题考查向量的投影,转化为向量的数量积和模长来运算是解决问题的关键,不等式恒成立问题,考查的知识点比较多,属基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 ,
, ,
,
 ;
; ”是“直线
”是“直线 与直线
与直线 相互垂直”的充要条件;
相互垂直”的充要条件; 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
; 的解集为R,则
的解集为R,则