题目内容
(本小题满分12分)
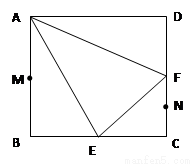
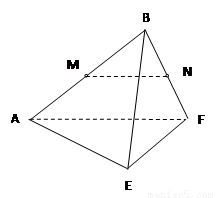
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
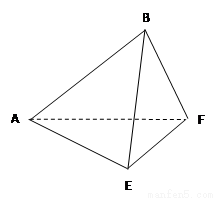
(Ⅰ)在三棱锥上标注出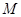 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ) 是线段
是线段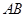 上一点,且
上一点,且 , 问是否存在点
, 问是否存在点 使得
使得 ,若存在,求出
,若存在,求出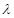 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
【答案】
(Ⅰ)因翻折后B、C、D重合,所以MN应是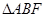 的一条中位线; 详见解析。
的一条中位线; 详见解析。
(Ⅱ)当点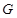 与点B重合时
与点B重合时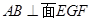 ,此时
,此时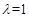 ;
;
(Ⅲ)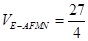 .
.
【解析】本试题是一个折叠图的运用。折叠图要关注不变量,然后利用空间的线面的位置关系判定线面平行和线面垂直问题,然后求解锥体的体积的运算的综合运用。
(1)因翻折后B、C、D重合,所以MN应是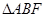 的一条中位线,且
的一条中位线,且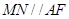 ,利用线面平行的判定定理得到结论。
,利用线面平行的判定定理得到结论。
(2)假设存在点G点使得AB垂直于平面EFG,那么先猜想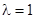 ,然后利用猜想证明得到结论。
,然后利用猜想证明得到结论。
(3)要求锥体的体积,要分析已知中的高,即线面垂直的性质定理的运用。
解:(Ⅰ)因翻折后B、C、D重合,所以MN应是 的一条中位线,如图所示.
的一条中位线,如图所示.
则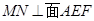 ………………2分
………………2分
证明如下: 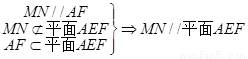 .…4分
.…4分
(Ⅱ)存在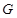 点使得
点使得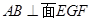 ,此时
,此时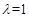
因为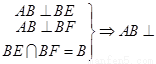 面EBF
面EBF
又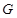 是线段
是线段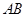 上一点,且
上一点,且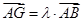 ,
,
∴ 当点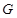 与点B重合时
与点B重合时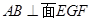 ,此时
,此时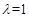 ………………8分
………………8分
(Ⅲ)因为
且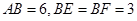 ,
,
∴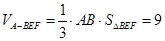 , ………………………………………9分
, ………………………………………9分
又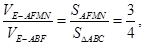 ………………………………11分
………………………………11分
∴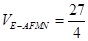 .
…………………………………12分
.
…………………………………12分

练习册系列答案
相关题目