题目内容
给出下列四个命题,其中真命题的序号为
(1)“直线a∥直线b”的必要不充分条件是“a平行于b所在的平面”;
(2)“直线l⊥平面α”的充要条件是“l垂直于平面α内的无数条直线”;
(3)“平面α∥平面β”是“α内有无数条直线平行于平面β”的充分不必要条件;
(4)“平面α⊥平面β”的充分条件是“有一条与α平行的直线l垂直于β”.
③④
③④
.(1)“直线a∥直线b”的必要不充分条件是“a平行于b所在的平面”;
(2)“直线l⊥平面α”的充要条件是“l垂直于平面α内的无数条直线”;
(3)“平面α∥平面β”是“α内有无数条直线平行于平面β”的充分不必要条件;
(4)“平面α⊥平面β”的充分条件是“有一条与α平行的直线l垂直于β”.
分析:利用必要条件、充分条件和充要条件的判断方法及平面平行于垂直的判定与性质结合题设条件知(3)(4)成立,利用必要条件、充分条件和充要条件的判断方法及线面平行于线面垂直的判定与性质得到(1)(2)不成立.
解答:解:对于(1),“直线a∥直线b”推不出“a平行于b所在的平面”;反之“a平行于b所在的平面”也不能推出直线a∥直线b,所以“直线a∥直线b”是“a平行于b所在的平面”;的既不充分也不必要条件故(1)不成立;
对于(2)“l⊥平面a”⇒“直线l⊥平面α内的所有直线;但“l垂直于平面α内的无数条直线”推不出“l⊥平面a”
故(2)不成立;
对于(3),“平面α∥平面β”能推出“α内有无数条直线平行于平面β”,但反之“α内有无数条直线平行于平面β”成立推不出“平面α∥平面β”,所以(3)对;
对于(4)“有一条与α平行的直线l垂直于β”成立,能推出α存在于l平行的直线垂直β,所以“平面α⊥平面β”所以(4)对
故答案为(3)(4).
对于(2)“l⊥平面a”⇒“直线l⊥平面α内的所有直线;但“l垂直于平面α内的无数条直线”推不出“l⊥平面a”
故(2)不成立;
对于(3),“平面α∥平面β”能推出“α内有无数条直线平行于平面β”,但反之“α内有无数条直线平行于平面β”成立推不出“平面α∥平面β”,所以(3)对;
对于(4)“有一条与α平行的直线l垂直于β”成立,能推出α存在于l平行的直线垂直β,所以“平面α⊥平面β”所以(4)对
故答案为(3)(4).
点评:本题考查必要条件、充分条件和充要条件的判断及空间中线、面的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目


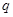 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与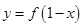 图像关于
图像关于 对称.
对称.