题目内容
已知函数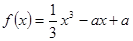
(Ⅰ)若函数 恰好有两个不同的零点,求
恰好有两个不同的零点,求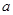 的值。
的值。
(Ⅱ)若函数 的图象与直线
的图象与直线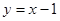 相切,求
相切,求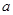 的值及相应的切点坐标。
的值及相应的切点坐标。
【解析】第一问中,利用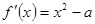
当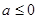 时,
时, 在
在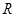 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当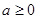 时,
时,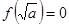 或
或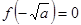 ,得
,得
第二问中,设切点为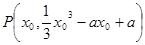 ,则
,则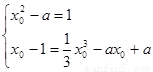
所以,当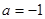 时,
时,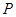 为
为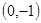 ;当
;当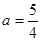 时,
时,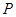 为
为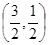
解:(Ⅰ)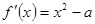 2分
2分
当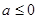 时,
时, 在
在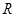 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当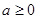 时,
时,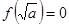 或
或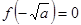 ,得
,得 4分
4分
(Ⅱ)设切点为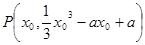 ,则
,则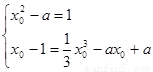 3分
3分
所以,当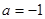 时,
时,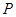 为
为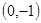 ;当
;当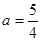 时,
时,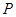 为
为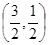
【答案】
(Ⅰ) (Ⅱ)当
(Ⅱ)当 时,
时, 为
为 ;当
;当 时,
时, 为
为

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
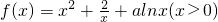 ,
,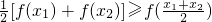 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.