题目内容
已知函数f(x)=ln (ax+1)+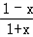 ,其中a>0.
,其中a>0.
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
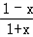 ,其中a>0.
,其中a>0.(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
解:(1)f(x)=ln (ax+1)+ 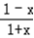 =ln(ax+1)+
=ln(ax+1)+ 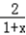 ﹣1,
﹣1,
求导函数可得f′(x)=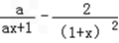 ,
,
∵f(x)在x=1处取得极值,
∴f'(1)=0,∴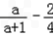 =0
=0
∴a=1;
(2)设f′(x)=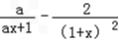 >0,有ax2>2﹣a,
>0,有ax2>2﹣a,
若a≥2,则f'(x)>0恒成立,f(x)在[0,+∞)上递增,
∴f(x)的最小值为f(0)=1;
若0<a<2,则x>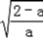 ,f'(x)>0恒成立,
,f'(x)>0恒成立,
f(x)在(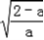 ,+∞)上递增,在(﹣∞,
,+∞)上递增,在(﹣∞,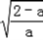 )上递减,
)上递减,
∴f(x)在x=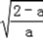 处取得最小值f(
处取得最小值f(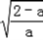 )<f(0)=1.
)<f(0)=1.
综上知,若f(x)最小值为1,则a的取值范围是[2,+∞).
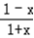 =ln(ax+1)+
=ln(ax+1)+ 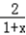 ﹣1,
﹣1,求导函数可得f′(x)=
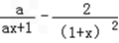 ,
, ∵f(x)在x=1处取得极值,
∴f'(1)=0,∴
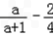 =0
=0∴a=1;
(2)设f′(x)=
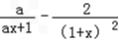 >0,有ax2>2﹣a,
>0,有ax2>2﹣a,若a≥2,则f'(x)>0恒成立,f(x)在[0,+∞)上递增,
∴f(x)的最小值为f(0)=1;
若0<a<2,则x>
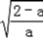 ,f'(x)>0恒成立,
,f'(x)>0恒成立,f(x)在(
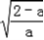 ,+∞)上递增,在(﹣∞,
,+∞)上递增,在(﹣∞,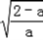 )上递减,
)上递减, ∴f(x)在x=
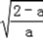 处取得最小值f(
处取得最小值f(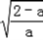 )<f(0)=1.
)<f(0)=1.综上知,若f(x)最小值为1,则a的取值范围是[2,+∞).

练习册系列答案
相关题目