题目内容
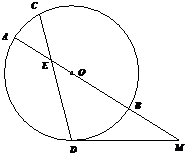 如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB=________,MB=________.
如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB=________,MB=________.
4 
分析:先根据相交弦定理得求出EB,即可求出OB;再结合切割线定理即可求出MB.
解答:由相交弦定理得:CE•ED=AE•EB? =6.
=6.
∴OB= =4.
=4.
又∵MD2=MB•MA=MB•(MB+BA).
设MB=x
∴16=X•(X+8)?x=-4+4 ,x=-4-4
,x=-4-4 (舍).
(舍).
故答案为:4,4 -4.
-4.
点评:本题主要考查与圆有关的比例线段、相交弦定理及切线性质的应用.属于基础题.考查计算能力.

分析:先根据相交弦定理得求出EB,即可求出OB;再结合切割线定理即可求出MB.
解答:由相交弦定理得:CE•ED=AE•EB?
 =6.
=6.∴OB=
 =4.
=4.又∵MD2=MB•MA=MB•(MB+BA).
设MB=x
∴16=X•(X+8)?x=-4+4
 ,x=-4-4
,x=-4-4 (舍).
(舍).故答案为:4,4
 -4.
-4.点评:本题主要考查与圆有关的比例线段、相交弦定理及切线性质的应用.属于基础题.考查计算能力.

练习册系列答案
相关题目
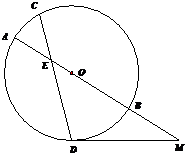 如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB=
如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB=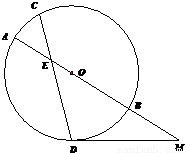 如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= .
如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= .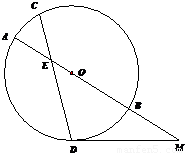 如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= .
如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= . 如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= .
如图,⊙O中的弦CD与直径AB相交于点E,M为AB延长线上一点,MD为⊙O的切线,D为切点,若AE=2,DE=4,CE=3,DM=4,则OB= ,MB= .