题目内容
已知数列{an}的前n项和Sn=(n2+n) 2n,则数列{ }的前n项和Tn=
}的前n项和Tn=
- A.(n-1)2n-2
- B.(n+2)2n-1
- C.(n+2)2n-2
- D.(n+2)2n+1-2
C
分析:由已知利用递推公式sn-sn-1=an,a1=s1可求通项,然后代入 ,利用错位相减即可求解数列的和
,利用错位相减即可求解数列的和
解答:∵Sn=(n2+n)﹒2n,
∴Sn-1=[(n-1)2+(n-1)]﹒2n-1,(n≥2)
两式相减可得,sn-sn-1=(n2+n)﹒2n-[(n-1)2+(n-1)]﹒2n-1,
=2n-1•(n2+3n)(n≥2)
n=1时,a1=s1=4适合上式
∴an=2n-1•(n2+3n)
∴ =(n+3)•2n-1
=(n+3)•2n-1
∴sn=4•20+5•2+…+(n+3)•2n-1
2sn=4•2+5•21+…+(n+2)•2n-1+(n+3)•2n
两式相减可得,-sn=4+2+22+…+2n-1-(n+3)•2n
=4+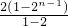 -(n+3)•2n
-(n+3)•2n
=4+2n-2-(n+3)•2n
=2-(n+2)•2n
∴Sn=(n+2)•2n-2
故选C.
点评:本题主要考查了数列的求和、利用数列的递推公式转化数列的和与项之间的关系,数列的错位相减求和方法的应用.
分析:由已知利用递推公式sn-sn-1=an,a1=s1可求通项,然后代入
 ,利用错位相减即可求解数列的和
,利用错位相减即可求解数列的和解答:∵Sn=(n2+n)﹒2n,
∴Sn-1=[(n-1)2+(n-1)]﹒2n-1,(n≥2)
两式相减可得,sn-sn-1=(n2+n)﹒2n-[(n-1)2+(n-1)]﹒2n-1,
=2n-1•(n2+3n)(n≥2)
n=1时,a1=s1=4适合上式
∴an=2n-1•(n2+3n)
∴
 =(n+3)•2n-1
=(n+3)•2n-1∴sn=4•20+5•2+…+(n+3)•2n-1
2sn=4•2+5•21+…+(n+2)•2n-1+(n+3)•2n
两式相减可得,-sn=4+2+22+…+2n-1-(n+3)•2n
=4+
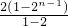 -(n+3)•2n
-(n+3)•2n=4+2n-2-(n+3)•2n
=2-(n+2)•2n
∴Sn=(n+2)•2n-2
故选C.
点评:本题主要考查了数列的求和、利用数列的递推公式转化数列的和与项之间的关系,数列的错位相减求和方法的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |