题目内容
若直线ax＋by＋1＝0(a、b>0)过圆x2＋y2＋8x＋2y＋1＝0的圆心，则
＋
的最小值为 ( )
| A．8 | B．12 | C．16 | D．20 |
C
解析
练习册系列答案
阅读快车系列答案
相关题目
与圆
（
）的公共弦长为
，则
_____.圆
与圆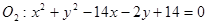
的位置关系是（ ）
| A．相离 | B．内含 | C．外切 | D．内切 |
直线
与圆
的位置关系为（ ）
| A．相切 | B．相交但直线不过圆心 |
| C．直线过圆心 | D．相离 |
若函数
的图象在点
处的切线
与圆
相交,则点
与圆
的位置关系是( )
| A．圆内 | B．圆内或圆外 | C．圆上 | D．圆外 |
若圆
上有且只有两个点到直线
的距离等于1，则半径
的取值范围是（ ）
| A．(4,6) | B． | C． | D． |
直线
截圆
得到的弦长为（ ）
A． | B． | C． | D． |
(O为坐标原点)等于 ( ▲ )点P(5a+1,12a)在圆(x－1)2+y2=1的内部，则a的取值范围是 （ ）
| A．｜a｜＜1 | B．a＜ | C．｜a｜＜ | D．｜a｜＜ |