题目内容
已知a1=9,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,…,设bn=lg(1+an).(1)证明数列{bn}是等比数列;
(2)设Cn=nbn+1,求数列{Cn}的前n项和;
(3)设dn=
| 1 |
| an |
| 1 |
| an+2 |
| 2 |
| an+1 |
| 2 |
| 9 |
分析:(1)把点(an,an+1)代入函数f(x)的解析式即可得an,an+1的关系式,两边取对数进而可得bn+1=2bn,原式得证,
(2)根据(1)中数列{bn}的首项和公比,可求得bn,进而可求得Cn,通过错位相减法求得数列{Cn}的前n项和,
(3)先根据an+1=an2+2an可推知
=
-
,进而求得dn与an+1和an的关系式,由(1)知:lg(1+an)=2n-1可求得an,代入dn与an+1和an的关系式,即可求得dn,由Dn=2(
-
)知Dn+
=
=
,进而证明Dn+
=
.
(2)根据(1)中数列{bn}的首项和公比,可求得bn,进而可求得Cn,通过错位相减法求得数列{Cn}的前n项和,
(3)先根据an+1=an2+2an可推知
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
| 2 |
| an+1 |
| 2 |
| a1 |
| 2 |
| 9 |
| 2 |
| an+1 |
| 2 |
| 9 |
解答:解:(1)证明:由题意知:an+1=an2+2an∴an+1+1=(an+1)2
∵a1=9,∴an+1>0,
∴lg(an+1+1)=lg(an+1)2即bn+1=2bn,
又∵b1=lg(1+a1)=1>0
∴{bn}是首项为1比为2的等比数列;
(2)由(1)知:bn=b1•2n-1=2n-1∴Cn=n•2n,设{Cn}的前n项和为Sn.
∴Sn=C1+C2+C3+…+Cn=1•21+2•22+3•23+…+n•2n
∴2Sn=1•22+2•23+3•24+…+(n-1)•2n+n•2n+1
-Sn=1•21+22+23+…+2n-n•2n+1=
-n•2n+1=2n+1-2-n•2n+1
∴Sn=n•2n+1-2n+1+2
{Cn}的前n项和为n•2n+1-2n+1+2.
(3)∵an+1=an2+2an=an(an+2)>0∴
=
(
-
)
∴
=
-
∴dn=
+
-
=2(
-
)
∴Dn=d1+d2+…+d n=2(
-
+
-
+…+
-
)=2(
-
)
又由(1)知:lg(1+an)=2n-1∴an+1=102n-1∴an+1=102n-1
∴Dn=2(
-
)又由Dn=2(
-
)知Dn+
=
=
.
∵a1=9,∴an+1>0,
∴lg(an+1+1)=lg(an+1)2即bn+1=2bn,
又∵b1=lg(1+a1)=1>0
∴{bn}是首项为1比为2的等比数列;
(2)由(1)知:bn=b1•2n-1=2n-1∴Cn=n•2n,设{Cn}的前n项和为Sn.
∴Sn=C1+C2+C3+…+Cn=1•21+2•22+3•23+…+n•2n
∴2Sn=1•22+2•23+3•24+…+(n-1)•2n+n•2n+1
-Sn=1•21+22+23+…+2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Sn=n•2n+1-2n+1+2
{Cn}的前n项和为n•2n+1-2n+1+2.
(3)∵an+1=an2+2an=an(an+2)>0∴
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+2 |
∴
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
∴Dn=d1+d2+…+d n=2(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| a1 |
| 1 |
| an+1 |
又由(1)知:lg(1+an)=2n-1∴an+1=102n-1∴an+1=102n-1
∴Dn=2(
| 1 |
| 9 |
| 1 |
| 102 n-1 |
| 1 |
| a1 |
| 1 |
| an+1 |
| 2 |
| an+1 |
| 2 |
| a1 |
| 2 |
| 9 |
点评:本题主要考查等比数列的性质和数列的求和.对于一些特殊数列的求和可利用错位相减法、裂项法等方法来解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.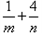 的最小值为
的最小值为