题目内容
9.已知函数f(x)=cos(-$\frac{x}{2}$)+sin($π-\frac{x}{2}$),x∈R(1)求函数f(x)的最小正周期与最大值
(2)求函数f(x)在[0,π)上单调递减区间.
分析 (1)根据条件将函数进行化简即可求函数f(x)的最小正周期与最大值.
(2)根据余弦函数的单调性进行求解即可.
解答 解:(1)f(x)=cos(-$\frac{x}{2}$)+sin($π-\frac{x}{2}$)=f(x)=cos$\frac{x}{2}$+cos$\frac{x}{2}$=2cos$\frac{x}{2}$,
则函数的周期T=$\frac{2π}{\frac{1}{2}}$=4π,
当cos$\frac{x}{2}$=1,设函数取得最大值2.
(2)由2kπ≤$\frac{x}{2}$≤2kπ+π,k∈Z,得4kπ≤x≤4kπ+2π,k∈Z,
当k=0时,0≤x≤2π,即此时函数为减函数,
故函数的减区间为[0,π).
点评 本题主要考查三角函数的图象和性质,利用条件将函数进行化简是解决本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
19.以(1,2)为圆心,$\sqrt{5}$为半径的圆的方程为( )
| A. | x2+y2-2x+4y=0 | B. | x2+y2+2x+4y=0 | C. | x2+y2-2x-4y=0 | D. | x2+y2+2x-4y=0 |
 某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.
某公园举办花展,其中一个展区平面图如图所示,中间区域是边长为10米的正方形ABCD,两侧区域分别是以AD、BC为直径的半圆,现在中间划出一个三角形区域MPQ,其中M为AB的中点,PQ∥AB,现有甲、乙两种花展出,甲种花的价格为2百元/平方米,填满三角形区域MPQ,乙种花的价格为4百元/平方米,填满其余区域.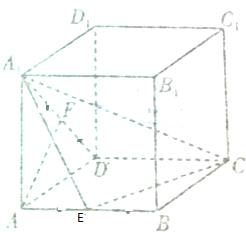 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.