题目内容
已知函数f(x)=2x+alnx(a∈R),
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个零点,求实数的取值范围;
(3)若函数f(x)的最小值为h(a),m,n为h(a)定义域A中的任意两个值,求证: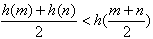 。
。
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个零点,求实数的取值范围;
(3)若函数f(x)的最小值为h(a),m,n为h(a)定义域A中的任意两个值,求证:
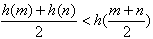 。
。 解:(1)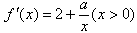 ,
,
令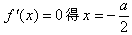 ,
,
当a≥0时,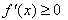 ,
,
∴函数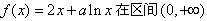 上单调递增;
上单调递增;
当a<0时,若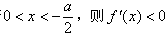 ;
;
若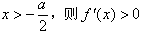 ;
;
∴函数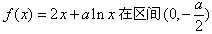 上单调递减,在区间
上单调递减,在区间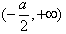 上单调递增;
上单调递增;
综上所述,当a≥0时,函数f(x)的单调增区间为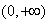 ;
;
当a<0时,函数f(x)的单调减区间为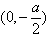 ,单调增区间为
,单调增区间为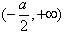 ;
;
(2)由(1)知,当a≥0时,函数f(x)至多有一个零点,不符合题意,
∴a<0,
又由(1)知,若a<0,
则函数f(x)在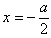 处取得极小值
处取得极小值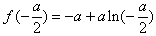 ,
,
∴函数f(x)有两个零点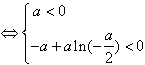 ,解得a<-2e,
,解得a<-2e,
∴a的取值范围是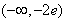 ;
;
(3)由(1)(2)知,当a≥0时,函数f(x)无最小值;
当a<0时,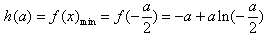 ,
,
对于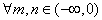 且m≠n,有
且m≠n,有
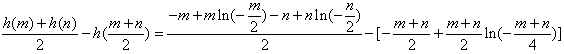
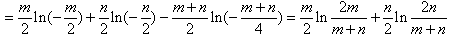 ,
,
不妨设m<n<0,则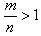 ,
,
令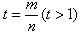 ,则
,则
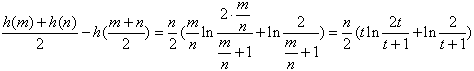 ,
,
设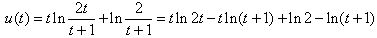 ,
,
则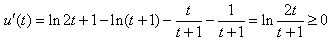 ,
,
当且仅当t=1时取“=”,
所以函数u(t)在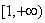 上单调递增,
上单调递增,
故t>1时,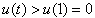 ,
,
又n<0,
∴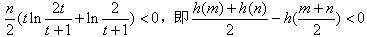 ,
,
所以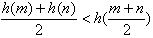 。
。
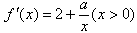 ,
,令
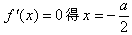 ,
,当a≥0时,
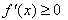 ,
,∴函数
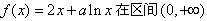 上单调递增;
上单调递增;当a<0时,若
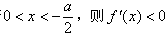 ;
;若
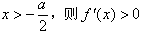 ;
;∴函数
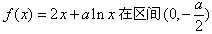 上单调递减,在区间
上单调递减,在区间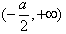 上单调递增;
上单调递增;综上所述,当a≥0时,函数f(x)的单调增区间为
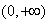 ;
;当a<0时,函数f(x)的单调减区间为
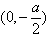 ,单调增区间为
,单调增区间为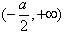 ;
;(2)由(1)知,当a≥0时,函数f(x)至多有一个零点,不符合题意,
∴a<0,
又由(1)知,若a<0,
则函数f(x)在
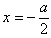 处取得极小值
处取得极小值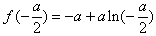 ,
,∴函数f(x)有两个零点
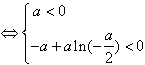 ,解得a<-2e,
,解得a<-2e,∴a的取值范围是
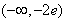 ;
;(3)由(1)(2)知,当a≥0时,函数f(x)无最小值;
当a<0时,
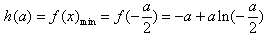 ,
,对于
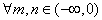 且m≠n,有
且m≠n,有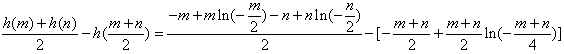
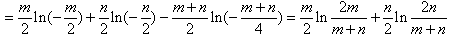 ,
,不妨设m<n<0,则
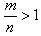 ,
,令
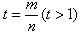 ,则
,则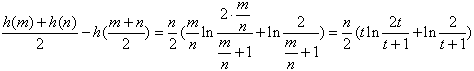 ,
,设
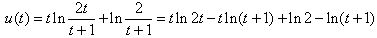 ,
,则
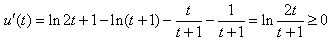 ,
,当且仅当t=1时取“=”,
所以函数u(t)在
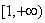 上单调递增,
上单调递增,故t>1时,
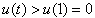 ,
,又n<0,
∴
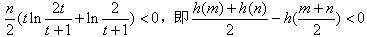 ,
,所以
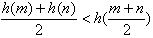 。
。 
练习册系列答案
相关题目